
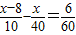 ,
,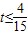 .
. 时,甲没有超过乙.
时,甲没有超过乙.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:
 说明理由.
说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
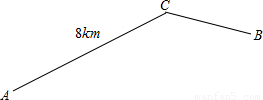
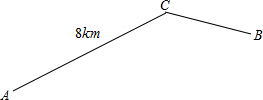 (2012•葫芦岛)如图,折线AC-BC是一条公路的示意图,AC=8km,甲骑摩托车从A地沿这条公路到B地,速度为40km/h,乙骑自行车从C地到B地,速度为10km/h,两人同时出发,结果甲比乙早到6分钟.
(2012•葫芦岛)如图,折线AC-BC是一条公路的示意图,AC=8km,甲骑摩托车从A地沿这条公路到B地,速度为40km/h,乙骑自行车从C地到B地,速度为10km/h,两人同时出发,结果甲比乙早到6分钟.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•路南区一模)已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.
(2012•路南区一模)已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:
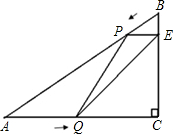
 (2012•成华区一模)如图,Rt△ABC中,∠C=90°,BC=3cm,AB=5cm.点P从点A出发沿AC以1.5cm/s的速度向点C匀速运动,到达点C后立刻以原来的速度沿CA返回;点Q从点B出发沿BA以1cm/s的速度向点A匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线PC-CB-BQ于点E.点P、Q同时出发,当点Q到达点A时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0),则当t=
(2012•成华区一模)如图,Rt△ABC中,∠C=90°,BC=3cm,AB=5cm.点P从点A出发沿AC以1.5cm/s的速度向点C匀速运动,到达点C后立刻以原来的速度沿CA返回;点Q从点B出发沿BA以1cm/s的速度向点A匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线PC-CB-BQ于点E.点P、Q同时出发,当点Q到达点A时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0),则当t=| 25 |
| 11 |
| 40 |
| 23 |
| 25 |
| 11 |
| 40 |
| 23 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com