Question

观察并探求下列各问题，写出你所观察得到的结论，并说明理由．
（1）如图，△ABC中，P为边BC上一点，试观察比较BP+PC与AB+AC的大小，并说明理由．

（2）将（1）中点P移至△ABC内，得图②，试观察比较△BPC的周长与△ABC的周长的大小，并说明理由．

（3）将（2）中点P变为两个点P₁、P₂得下图，试观察比较四边形BP₁P₂C的周长与△ABC的周长的大小，并说明理由．

（4）将（3）中的点P₁、P₂移至△ABC外，并使点P₁、P₂与点A在边BC的异侧，且∠P₁BC＜∠ABC，∠P₂CB＜∠ACB，得图，试观察比较四边形BP₁P₂C的周长与△ABC的周长的大小，并说明理由．

（5）若将（3）中的四边形BP₁P₂C的顶点B、C移至△ABC内，得四边形B₁P₁P₂C₁，如图⑤，试观察比较四边形B₁P₁P₂C₁的周长与△ABC的周长的大小，并说明理由．

Answer 1

解：（1）BP+PC＜AB+AC，理由：三角形两边之和大于第三边，或两点之间线段最短．

（2）△BPC的周长＜△ABC的周长．理由：
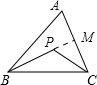
如图，延长BP交AC于M，在△ABM中，BP+PM＜AB+AM，在△PMC中，PC＜PM+MC，两式相加得BP+PC＜AB+AC，于是得：△BPC的周长＜△ABC的周长．

（3）四边形BP₁P₂C的周长＜△ABC的周长．理由：
如图，分别延长BP₁、CP₂交于M，由（2）知，BM+CM＜AB+AC，又P₁P₂＜P₁M+P₂M，可得，BP₁+P₁P₂+P₂C＜BM+CM＜AB+AC，可得结论．
或：作直线P₁P₂分别交AB、AC于M、N（如图），△BMP₁中，BP₁＜BM+MP₁，△AMN中，MP₁+P₁P₂+P₂M＜AM+AN，△P₂NC中，P₂C＜P₂N+NC，三式相加得：BP₁+P₁P₂+P₂C＜AB+AC，可得结论．

（4）四边形BP₁P₂C的周长＜△ABC的周长．理由如下：将四边形BP₁P₂C沿直线BC翻折，使点P₁、P₂落在△ABC内，转化为（3）情形，即可．
（5）比较四边形B₁P₁P₂C₁的周长＜△ABC的周长．理由如下：
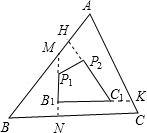
如图，分别作如图所示的延长线交△ABC的边于M、N、K、H，在△BNM中，NB₁+B₁P1+P₁M＜BM+BN，又显然有，B₁C₁+C₁K＜NB₁+NC+CK，及C₁P₂+P₂H＜C₁K+AK+AH，及P₁P₂＜P₂H+MH+P₁M，将以上各式相加，得B₁P₁+P₁P₂+P₂C+B₁C₁＜AB+BC+AC，于是得结论．

分析：（1）、（2）、（3）通过作辅助线，利用三角形的第三边小于两边之和，大于两边之差进行解答；
（4）通过将四边形BP₁P₂C沿直线BC翻折，使点P₁、P₂落在△ABC内，转化为（3）情形，从而问题得解；
（5）延长B₁P₁、C₁P₂分别与AB相交，再利用三角形的第三边小于两边之和，大于两边之差进行解答．
点评：比较线段的长短常常利用三角形的三边关系以及不等式的性质，通过作辅助线进行解答．