
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=![]() 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积![]() =4.
=4.
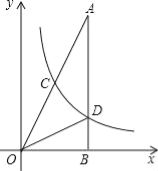
(1)求直线AO的解析式;
(2)求反比例函数解析式;
(3)求点C的坐标.
【答案】(1)y=2x;(2)y=![]() ;(3)(2,4)
;(3)(2,4)
【解析】
试题分析:(1)首先根据题意确定A点坐标,然后设直线AO的解析式为y=kx,再把A点坐标代入可得k的值,进而可得函数解析式;
(2)根据△BOD的面积![]() =4可得D点坐标,再把D点坐标代入y=
=4可得D点坐标,再把D点坐标代入y=![]() 可得k的值,进而可得函数解析式;
可得k的值,进而可得函数解析式;
(3)点C是正比例函数和反比例函数的交点,联立两个函数解析式,然后再解可得C点坐标.
试题解析:(1)∵OB=4,AB=8,∠ABO=90°,
∴A点坐标为(4,8),
设直线AO的解析式为y=kx,
则4k=8,解得k=2,
即直线AO的解析式为y=2x;
(2)∵OB=4,S△BOD=4,∠ABO=90°,
∴D点坐标为(4,2),
点D(4,2)代入y=![]() ,
,
则2=![]() ,解得k=8,
,解得k=8,
∴反比例函数解析式为y=![]() ;
;
(3)直线y=2x与反比例函数y=![]() 构成方程组为
构成方程组为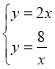 ,
,
解得 ,
,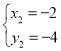 (舍去),
(舍去),
∴C点坐标为(2,4).


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】某种植物的主干长出若干数目的支干,每个支干又长出相同数目的小分支,若小分支、支干和主干的总数目是73,则每个支干长出的小分支的数目为( )
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知不等边三角形的两边长分别是2cm和9cm,如果第三边的长为整数,那么第三边的长为( )
A.8cm
B.10cm
C.8cm或10cm
D.8cm或9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.

证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目 (被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
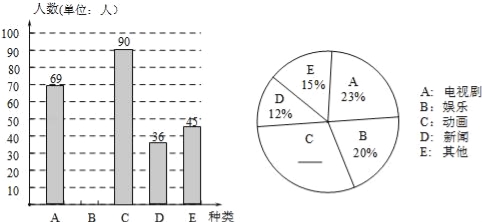
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有2000名学生,请估计该校喜爱电视剧节目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,解答后面提出的问题:
黑白双雄,纵横江湖;双剑合壁,天下无敌,这是武侠小说中的常见描述,其意思是指两个人合在一起,取长补短,威力无比,在二次根式中也有这种相辅相成的“对子”,如:(2+![]() )(2-
)(2-![]() )=1,(
)=1,(![]() +
+![]() )(
)(![]() -
-![]() )=3, 它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
)=3, 它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:![]() =
=![]() =
=![]() ,
,![]() =
=![]() =7+4
=7+4![]() .像这样通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
.像这样通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
解决问题:
(1)4+![]() 的有理化因式是 ,将
的有理化因式是 ,将![]() 分母有理化得 ;
分母有理化得 ;
(2)已知x=![]() ,y=
,y=![]() ,则
,则![]() = ;
= ;
(3)已知实数x,y满足(x+![]() )(y+
)(y+![]() )-2017=0,则x= ,y= .
)-2017=0,则x= ,y= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com