
分析 (1)把点A坐标代入反比例函数解析式中,即可求出k的值;
(2)联立两个函数解析式,求出x的值即可;
(3)根据图象即可求出满足条件的x的取值范围.
解答 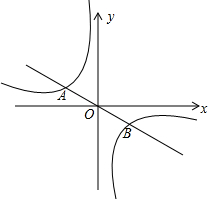 解:(1)∵正比例函数y1=-$\frac{1}{2}$x与反比例函数y2=$\frac{k}{x}$的图象经过A(-2,1)点,
解:(1)∵正比例函数y1=-$\frac{1}{2}$x与反比例函数y2=$\frac{k}{x}$的图象经过A(-2,1)点,
∴k=-2,
∴y2=$\frac{-2}{x}$,
(2)∵正比例函数y1=-$\frac{1}{2}$x与反比例函数y2=$\frac{-2}{x}$的图象有两个交点,
∴$\frac{-x}{2}$=$\frac{-2}{x}$,
∴x2=4,即x=±2,
∴正比例与反比例函数另一个交点B的坐标为(2,-1),
(3)根据图象可知,当x=±2时,y1=y2,当-2<x<0或x>2时,y1<y2,当x<-2或0<x<2时,y1>y2.
点评 本题考查了反比例函数和一次函数的图象.无论是求自变量的取值范围还是函数值的取值范围,都应该从交点入手思考.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
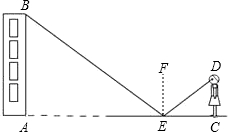 小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20m.当她与镜子的距离CE=2.5m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.5m,请你帮助小红计算大楼的高度.
小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20m.当她与镜子的距离CE=2.5m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.5m,请你帮助小红计算大楼的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
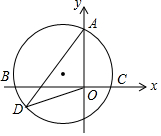 如图,在直角坐标系中,已知点A(0,4),B(-4,0),C(2,0),过A,B,C作外接圆,D为圆上一动点,求$\sqrt{5}$DO+DA的最小值.
如图,在直角坐标系中,已知点A(0,4),B(-4,0),C(2,0),过A,B,C作外接圆,D为圆上一动点,求$\sqrt{5}$DO+DA的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
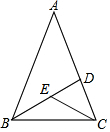 如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别平分∠ABC,∠ACB,若CD=3,则CE等于( )
如图,在△ABC中,AB=AC,∠A=36°,BD,CE分别平分∠ABC,∠ACB,若CD=3,则CE等于( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 3.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com