
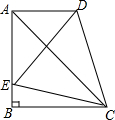
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交AC于H.下列结论:①△ACD≌△ACE;②∠ACD=30°;③A、C两点关于DE所在直线对称;④$\frac{{S}_{△AEH}}{{S}_{△CDH}}$=$\frac{EH}{CD}$.其中正确的结论是①②.(把你认为正确的结论的序号都填上)
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交AC于H.下列结论:①△ACD≌△ACE;②∠ACD=30°;③A、C两点关于DE所在直线对称;④$\frac{{S}_{△AEH}}{{S}_{△CDH}}$=$\frac{EH}{CD}$.其中正确的结论是①②.(把你认为正确的结论的序号都填上) 分析 ①根据等腰直角三角形的性质,可得∠BAC=∠DAC=$\frac{1}{2}$∠BAC=45°,根据SAS,可得答案;
②根据角的和差,可得∠ACE的度数,根据全等三角形的性质,可得答案;
③根据线段垂直平分线的判定,可得答案;
④根据三角形的面积公式,可得答案.
解答 解:如图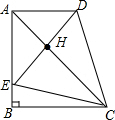
①AD∥BC,∠ABC=90°,AB=BC,∠BAC=∠DAC=$\frac{1}{2}$∠BAC=45°,在△ACD和△ACE中$\left\{\begin{array}{l}{AD=AE}\\{∠DAC=∠EAC=45°}\\{AC=AC}\end{array}\right.$,∴△ACD≌△ACE,故①正确;
②∠ACE=∠ACB-∠BCE=45°-15°=30°,∵△ACD≌△ACE,∴∠ACD=∠ACE=30°,故②正确;
③∵∠HDA=∠DAH=∠HAE=∠AEH-45°,AH=DH;∵∠DCH=30°,∠CHD=60°,∴CH>DH,∴CH>AH,故③错误;
④$\frac{{S}_{△AEH}}{{S}_{△CDH}}$=$\frac{\frac{1}{2}AH•EH}{\frac{1}{2}DH•CH}$=$\frac{AH}{CH}$≠$\frac{EH}{CD}$,故④错误;
故答案为:①②.
点评 本题考查了全等三角形的判定与性质,利用直角三角形的性质得出∠DAC=∠EAC=45°是解题关键,利用了全等三角形的判定与性质,线段垂直平分线的判定,三角形的面积公式.


科目:初中数学 来源: 题型:解答题
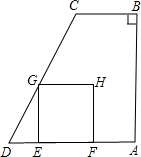 如图,梯形ABCD中,CB∥DA,∠ABC=90°,BA=AD=4,BC=2.动点E从点D出发,以每秒1个单位的速度沿线段DA运动,到点A停止,过点E作EG⊥AD交折线D-C-B于点G,以GE为一边向右作正方形GEFH.设运动时间为t(秒),正方形GEFH与梯形ABCD重叠面积为S(平方单位).
如图,梯形ABCD中,CB∥DA,∠ABC=90°,BA=AD=4,BC=2.动点E从点D出发,以每秒1个单位的速度沿线段DA运动,到点A停止,过点E作EG⊥AD交折线D-C-B于点G,以GE为一边向右作正方形GEFH.设运动时间为t(秒),正方形GEFH与梯形ABCD重叠面积为S(平方单位).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
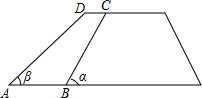 如图,沿水库拦水坝的背水坡将坝面加宽CD=2米,坡度由原来的$\sqrt{3}$:1改为1:1,已知背水坡BC长12米.
如图,沿水库拦水坝的背水坡将坝面加宽CD=2米,坡度由原来的$\sqrt{3}$:1改为1:1,已知背水坡BC长12米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c=2a+b | B. | c=a+2b | C. | c=2b-a | D. | c=2a-b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com