

���� ��1������ƽ�Ƶ����ʵó�ֱ��OD�Ľ���ʽΪy=x�������߶�CAƽ�Ƶ�OD����C��-1��2����A��m��m+3�����ó�D��m+1��m+1����
��2���跴������������ʽΪy=$\frac{k}{x}$����A��m��m+3����D��m+1��m+1�����ڷ���������ͼ���ϣ��ó�m��m+3��=��m+1����m+1������ã�m=1���ɣ�
��3����ֱ��y=x+3����ƽ��6����λ��ֱ��y=x-3���ⷽ����$\left\{\begin{array}{l}{y=\frac{4}{x}}\\{y=x-3}\end{array}\right.$���ɵó��𰸣�
��4��������������ٵ�O'C'��AD�����ʱ�������ε����ʺ��ɶ����ó�O'D=AD=O'C'=OC=$\sqrt{5}$��OD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$�����OO'=2$\sqrt{2}$-$\sqrt{5}$���ɣ�
�ڵ�O'C'��AD�����ʱ��ͬ���ó�OO'=2$\sqrt{2}$+$\sqrt{5}$���ó�t=2$\sqrt{2}$-$\sqrt{5}$���ɣ�
��� �⣺��1�����߶�OD����ֱ������ֱ��y=x+3ƽ�Ƶõ��ģ�
��ֱ��OD�Ľ���ʽΪy=x��
���߶�CAƽ�Ƶ�OD����C��-1��2����A��m��m+3����
��D��m+1��m+3-2����
��D��m+1��m+1����
�ʴ�Ϊ����m+1��m+1����
��2���跴������������ʽΪy=$\frac{k}{x}$��
��A��m��m+3����D��m+1��m+1�����ڷ���������ͼ���ϣ�
��m��m+3��=��m+1����m+1����
��ã�m=1��
��A��1��4����D��2��2����
��k=1��4=4��
�෴������������ʽΪy=$\frac{4}{x}$��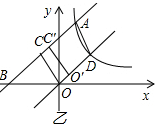
��3����ֱ��y=x+3����ƽ��6����λ��ֱ��y=x-3��
�ⷽ����$\left\{\begin{array}{l}{y=\frac{4}{x}}\\{y=x-3}\end{array}\right.$�ã�$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$��$\left\{\begin{array}{l}{x=-1}\\{y=-4}\end{array}\right.$����ȥ����
��E��4��1����
��4��������������ٵ�O'C'��AD�����ʱ����ͼ����ʾ��
���ı���O'C'OD�����Σ�
��O'D=AD=O'C'=OC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$��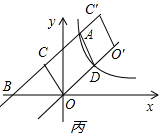
��OD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$��
��OO'=OD-O'D=2$\sqrt{2}$-$\sqrt{5}$��
���߶�OC��ÿ��1����λ���ȵ��ٶ���������CA�ķ���ƽ����O��C�䣬
��t=2$\sqrt{2}$-$\sqrt{5}$��
�ڵ�O'C'��AD�����ʱ����ͼ����ʾ��
ͬ���ó�OO'=2$\sqrt{2}$+$\sqrt{5}$��
��t=2$\sqrt{2}$-$\sqrt{5}$��
������������tΪ2$\sqrt{2}$-$\sqrt{5}$��2$\sqrt{2}$+$\sqrt{5}$ʱ����O�䣬C�䣬A��DΪ������ı��������Σ�
���� �����Ƿ����������ۺ���Ŀ�������˷�������������ʽ����������ͼ�����ʡ�ƽ�Ƶ����ʡ����ɶ�����ֱ����˫���ߵĽ��㡢���ε����ʡ��ⷽ�����֪ʶ�������ۺ���ǿ����һ���Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x+2y=5xy | B�� | ��m2��3=m5 | C�� | ��3a-b��2=9a2-b2 | D�� | x3��x=x2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 | B�� | 12 | C�� | 36 | D�� | 144 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
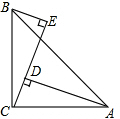 ��ͼ����ACB=90�㣬AC=BC��AD��CE��BE��CE������ΪD��E����ô�����߶�BE��DE��AD֮���������ϵΪAD-BE=DE��
��ͼ����ACB=90�㣬AC=BC��AD��CE��BE��CE������ΪD��E����ô�����߶�BE��DE��AD֮���������ϵΪAD-BE=DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | С�� | С�� | Сӱ | С�� | С�� |
| ����/kg | -6 | +5 | -4 | +8 | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com