
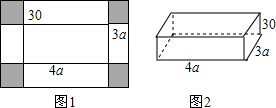
分析 (1)根据图形表示出原长方形铁皮的面积即可;
(2)根据原长方形铁皮的面积剪去四个小正方形的面积,求出铁盒的表面积,乘以单价即可得到结果;
(3)用铁盒的底面积除以全面积即可得出底面积是全面积的几分之几,再根据铁盒的底面积是全面积的$\frac{3}{4}$,求出a的值即可;
(4)假设存在,列出铁盒的全面积和底面积的公式,求整数倍数即可.
解答 解:(1)原铁皮的面积是(4a+60)(3a+60)=12a2+420a+3600;
(2)油漆这个铁盒的表面积是:12a2+2×30×4a+2×30×3a=12a2+420a,
则油漆这个铁盒需要的钱数是:(12a2+420a)÷$\frac{a}{50}$=(12a2+420a)×$\frac{50}{a}$=600a+21000(元);
(3)铁盒的底面积是全面积的$\frac{12{a}^{2}}{12{a}^{2}+420a}$=$\frac{a}{a+35}$;
根据题意得:$\frac{a}{a+35}$=$\frac{3}{4}$,
解得a=105;
(4)铁盒的全面积是4a×3a+4a×30×2+3a×30×2=12a2+420a,
底面积是12a2,
假设存在正整数n,使12a2+420a=n(12a2)
则(n-1)a=35,
则a=35,n=2或a=7,n=6或a=5,n=8或a=1,n=36
所以存在铁盒的全面积是底面积的正整数倍,这时a=35或7或5或1.
点评 此题考查整式的混合运算,掌握正方体的全面积与底面积的计算方法是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
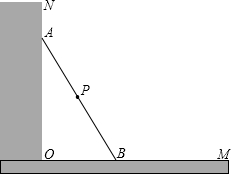 如图所示,一根长3米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上.设木棍的中点为P.若木棍A端沿墙下滑.且B端沿地面向右滑行.
如图所示,一根长3米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上.设木棍的中点为P.若木棍A端沿墙下滑.且B端沿地面向右滑行.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
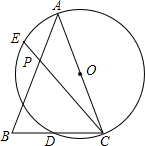 如图,在△ABC中,已知AB=AC,∠B=70°,以AC为直径作⊙O交BC于点D,弦CE交AB于点P,且∠ACE=20°,则$\frac{AP}{BC}$的值是( )
如图,在△ABC中,已知AB=AC,∠B=70°,以AC为直径作⊙O交BC于点D,弦CE交AB于点P,且∠ACE=20°,则$\frac{AP}{BC}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com