
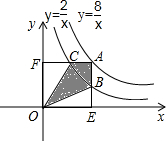 如图,A是双曲线
如图,A是双曲线 上的点,过点A作AE⊥x轴于点E,作AF⊥y轴于点F,AE、AF与双曲线
上的点,过点A作AE⊥x轴于点E,作AF⊥y轴于点F,AE、AF与双曲线 分别交于点B、C,则四边形ABOC的面积是
分别交于点B、C,则四边形ABOC的面积是 中求出ab的值,而矩形AEOF的面积等于AE与AF的乘积,即为ab的值,确定出矩形AEOF的面积,设出C和B的坐标,同理求出三角形OCF与三角形BOE的面积,用矩形AEOF的面积-三角形OCF的面积-三角形BOE的面积,即可得到四边形ABOC的面积.
中求出ab的值,而矩形AEOF的面积等于AE与AF的乘积,即为ab的值,确定出矩形AEOF的面积,设出C和B的坐标,同理求出三角形OCF与三角形BOE的面积,用矩形AEOF的面积-三角形OCF的面积-三角形BOE的面积,即可得到四边形ABOC的面积. 得:ab=8,
得:ab=8, 得:mn=2,
得:mn=2, CF•OF=
CF•OF= mn=1,
mn=1, (k≠0)图象上的点作两坐标轴的垂线,两垂线与两坐标轴围成矩形的面积等于|k|,熟练掌握此性质是解本题的关键.
(k≠0)图象上的点作两坐标轴的垂线,两垂线与两坐标轴围成矩形的面积等于|k|,熟练掌握此性质是解本题的关键. 

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
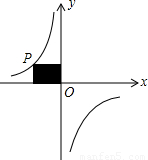
 (2013•清远模拟)如图点P是双曲线上的一点,过P点分别向x轴,y轴引垂线,得到图中的阴影部分的矩形面积为3,则这个反比例函数的表达式为
(2013•清远模拟)如图点P是双曲线上的一点,过P点分别向x轴,y轴引垂线,得到图中的阴影部分的矩形面积为3,则这个反比例函数的表达式为| 3 |
| x |
| 3 |
| x |
查看答案和解析>>
科目:初中数学 来源:2013年广东省清远市清新区中考数学模拟试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com