Question

如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC＝BD．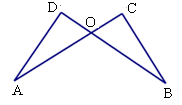

求证：（1）BC＝AD；
（2）△OAB是等腰三角形．

Answer 1

（1）证明边相等，首选全等三角形。该题已知条件，可以连接AB，有公共边AB，因为有一角是直角，可以用HL证明，因为有AC＝BD，所以BC＝AD；
（2）证明等腰三角形，除了直接证明腰相等，还可以证明底角相等，由（1）得对应角∠CAB＝∠DBA，所以OA＝OB，即△OAB是等腰三角形.

解析试题分析：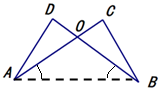
（1）连接BA，∵AC⊥BC，BD⊥AD，
∴在R t △DAB与R t △CAB中，AC=DB  AB=AB
∴R t △DAB ≌ R t △CAB （HL）
∴BC＝AD
(2)∵R t △DAB ≌ R t △CAB(已证)
∴∠CAB＝∠DBA
∴OA＝OB，
∴△OAB是等腰三角形．
考点：等腰三角形
点评：该题较为简单，是常考题，树妖考查学生对全等三角形和等腰三角形的判定的理解和应用能力。