（2013•鼓楼区一模）问题提出：
规定：四条边对应相等，四个角对应相等的两个四边形全等．
我们借助学习“三角形全等的判定”获得的经验与方法对“全等四边形的判定”进行探究．
初步思考：
在两个四边形中，我们把“一条边对应相等”或“一个角对应相等”称为一个条件．满足4个条件的两个四边形不一定全等，如边长相等的正方形与菱形就不一定全等．类似地，我们容易知道两个四边形全等至少需要5个条件．
深入探究：
小莉所在学习小组进行了研究，她们认为5个条件可分为以下四种类型：
Ⅰ一条边和四个角对应相等；Ⅱ二条边和三个角对应相等；
Ⅲ三条边和二个角对应相等；Ⅳ四条边和一个角对应相等．
（1）小明认为“Ⅰ一条边和四个角对应相等”的两个四边形不一定全等，请你举例说明．
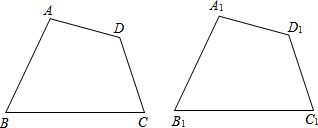
（2）小红认为“Ⅳ四条边和一个角对应相等”的两个四边形全等，请你结合下图进行证明．
已知：如图，
四边形ABCD和四边形A1B1C1D1中，AB=A1B1，BC=B1C1，CD=C1D1，DA=D1A1，∠B=∠B1．
四边形ABCD和四边形A1B1C1D1中，AB=A1B1，BC=B1C1，CD=C1D1，DA=D1A1，∠B=∠B1．
．
求证：
四边形ABCD≌四边形A1B1C1D1
四边形ABCD≌四边形A1B1C1D1
．
证明：
（3）小刚认为还可以对“Ⅱ二条边和三个角对应相等”进一步分类，他以四边形ABCD和四边形A
1B
1C
1D
1为例，分为以下几类：
①AB=A
1B
1，AD=A
1D
1，∠A=∠A
1，∠B=∠B
1，∠C=∠C
1；
②AB=A
1B
1，AD=A
1D
1，∠A=∠A
1，∠B=∠B
1，∠D=∠D
1；
③AB=A
1B
1，AD=A
1D
1，∠B=∠B
1，∠C=∠C
1，∠D=∠D
1；
④AB=A
1B
1，CD=C
1D
1，∠A=∠A
1，∠B=∠B
1，∠C=∠C
1．
其中能判定四边形ABCD和四边形A
1B
1C
1D
1全等的是
①②③
①②③
（填序号），概括可得“全等四边形的判定方法”，这个判定方法是
有一组邻边和三个角对应相等的两个四边形全等
有一组邻边和三个角对应相等的两个四边形全等
．
（4）小亮经过思考认为也可以对“Ⅲ三条边和二个角对应相等”进一步分类，请你仿照小刚的方法先进行分类，再概括得出一个全等四边形的判定方法．
解：如图所示，CD、EF为路灯高度，AB为该人高度，BM、BN为该人前后的两个影子．
