
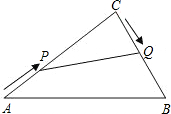
 在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.
在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.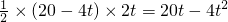 cm2;
cm2;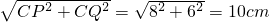 ;
; ,即
,即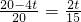 ,解得t=3秒;
,解得t=3秒;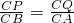 ,即
,即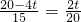 ,解得t=
,解得t= 秒.
秒. 秒时,以点C、P、Q为顶点的三角形与△ABC相似.
秒时,以点C、P、Q为顶点的三角形与△ABC相似. CP×CQ求解;
CP×CQ求解;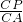 =
=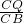 ,可将时间t求出;当Rt△CPQ∽Rt△CBA时,根据
,可将时间t求出;当Rt△CPQ∽Rt△CBA时,根据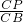 =
=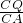 ,可求出时间t.
,可求出时间t.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com