
| 68 |
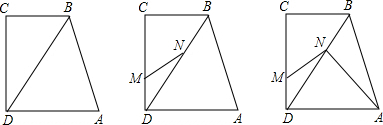
| 2 |
| 5 |
| 10 |
| 3 |
| 2 |
| 5 |
| 10 |
| 3 |
| 3 |
| 5 |
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
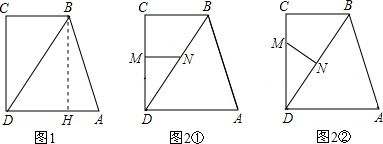 解:(1)如图1,过点B作BH⊥AD于点H,则四边形DHBC为矩形,BH=CD=8.
解:(1)如图1,过点B作BH⊥AD于点H,则四边形DHBC为矩形,BH=CD=8.| 68 |
(
|
| 62+82 |
| DM |
| DN |
| CD |
| BD |
| t |
| 10-t |
| 8 |
| 10 |
| 40 |
| 9 |
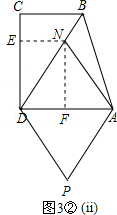
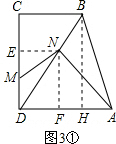 ②当∠MND=90°时,如图2②.
②当∠MND=90°时,如图2②.| DN |
| DM |
| CD |
| BD |
| 10-t |
| t |
| 8 |
| 10 |
| 50 |
| 9 |
| 40 |
| 9 |
| 50 |
| 9 |
| EN |
| DN |
| BC |
| BD |
| EN |
| 10-t |
| 6 |
| 10 |
| 3 |
| 5 |
| NF |
| DN |
| BH |
| BD |
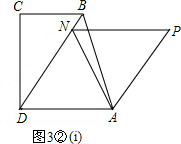 ∴
∴| NF |
| 10-t |
| 8 |
| 10 |
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| 3 |
| 10 |
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
| 10 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
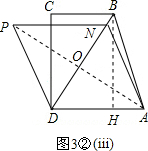 在Rt△AOD中,∵∠AOD=90°,
在Rt△AOD中,∵∠AOD=90°,| 6 |
| 10 |
| 24 |
| 5 |
| 1 |
| 2 |
| 24 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 10 |
| 3 |
| 2 |
| 5 |
| 10 |
| 3 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com