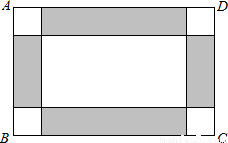
解:(1)设小正方形的边长为x米,
则4x
2+(10-2x)(8-2x)=52,
整理得:2x
2-9x+7=0,即(x-1)(2x-7)=0,
解得:x
1=1,x
2=3.5,
经检验均符合题意,
答:小正方形的边长为1米或3.5米;
(2)设铺设地面的总费用为W元,
则W=30×[4x
2+(10-2x)(8-2x)]+20×[10×8-4x
2-(10-2x)(8-2x)]
=80x
2-360x+2400=80(x-

)
2+1995,
∵80>0,∴W有最小值,
当x=

米时,W
最小值=1995元.
答:当小正方形的边长为

米时,铺设地面的总费用最少,最少费用为1995元.
分析:(1)设小正方形的边长为x米,表示出里边大矩形的长为(10-2x)米,宽为(8-2x)米,利用白色部分的面积=4个小正方形的面积+里边大矩形的面积,列出关于x的方程,求出方程的解得到x的值,即为小正方形的边长;
(2)设铺设底面的总费用为W,由(1)表示出的白色部分的面积,根据矩形ABCD的面积-白色部分的面积=绿色部分的面积,根据各自的单价表示出铺设底面的总费用,得到W与x的二次函数,根据二次函数的性质即可求出铺设总费用的最小值及此时小正方形的边长.
点评:此题考查了二次函数的应用,以及一元二次方程的应用,涉及的知识有:二次函数的性质,一元二次方程的解法,配方法的应用,以及二次函数的图象与性质,弄清题中的等量关系是解本题第一问的关键.

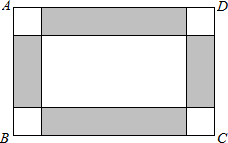 部分铺白色地面砖.
部分铺白色地面砖. )2+1995,
)2+1995, 米时,W最小值=1995元.
米时,W最小值=1995元. 米时,铺设地面的总费用最少,最少费用为1995元.
米时,铺设地面的总费用最少,最少费用为1995元.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案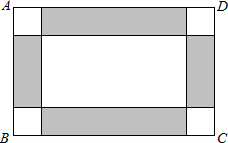 部分铺白色地面砖.
部分铺白色地面砖.