
【题目】如图,点![]() 、
、![]() 为直线
为直线![]() 上的两点,过
上的两点,过![]() 、
、![]() 两点分别作
两点分别作![]() 轴的平行线交双曲线
轴的平行线交双曲线![]() (x>0)于点
(x>0)于点![]() 、
、![]() 两点.若
两点.若![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
延长AC交x轴于E,延长BD交x轴于F.设A、B的横坐标分别是a,b,点A、B为直线y=x上的两点,A的坐标是(a,a),B的坐标是(b,b).则AE=OE=a,BF=OF=b.根据BD=2AC即可得到a,b的关系,然后利用勾股定理,即可用a,b表示出所求的式子从而求解.
 延长AC交x轴于E,延长BD交x轴于F.
延长AC交x轴于E,延长BD交x轴于F.
设A.B的横坐标分别是a,b,
∵点A.B为直线y=x上的两点,
∴A的坐标是(a,a),B的坐标是(b,b).则AE=OE=a,BF=OF=b.
∵C、D两点在交双曲线y=1x(x>0)上,则CE=![]() ,DF=
,DF=![]() .
.
∴BD=BFDF=b![]() ,AC=a
,AC=a![]() .
.
又∵BD=2AC
∴b1b=2(a![]() ),
),
两边平方得:b2+![]() 2=4(a2+
2=4(a2+![]() 2),即b2+
2),即b2+![]() =4(a2+
=4(a2+![]() )6.
)6.
在直角△OCE中,OC2=OE2+CE2=a2+![]() ,同理OD2=b2+
,同理OD2=b2+![]() ,
,
∴4OC20D2=4(a2+![]() )(b2+
)(b2+![]() )=6,
)=6,
故选B.


科目:初中数学 来源: 题型:
【题目】解下列方程.
(1)2(1-x)2-8=0 (2 )2x2![]() x-1=0 (公式法)
x-1=0 (公式法)
(3)x2-3x+1=0(配方法) (4) (x-1)2-5(x-1)+6=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图,在正方形![]() 和平行四边形
和平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
探究:当![]() 与
与![]() 的夹角为多少度时,平行四边形
的夹角为多少度时,平行四边形![]() 是正方形?
是正方形?
小聪同学的思路是:首先可以说明四边形![]() 是矩形;然后延长
是矩形;然后延长![]() 交
交![]() 于点
于点![]() ,构造全等三角形,经过推理可以探索出问题的答案.
,构造全等三角形,经过推理可以探索出问题的答案.
请你参考小聪同学的思路,探究并解决这个问题.

(1)求证:四边形![]() 是矩形;
是矩形;
(2)![]() 与
与![]() 的夹角为________度时,四边形
的夹角为________度时,四边形![]() 是正方形.
是正方形.
理由:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,AB 两点的坐标分别为 A(1,4),B(5,1),P,Q 分别是 x 轴,y 轴 上两个动点,则四边形 ABPQ 的周长最小值为( )
A.5B.5 ![]() C.
C.![]()
![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期初,某校为迎接中华人民共和国建国七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代”为主题的读书活动。校德育处对本校七年级学生四月份“阅读该主题相关书籍的读书量”(下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,如下图所示:

根据以上信息,解答下列问题:
(1)补全上面两幅统计图,填出本次所抽取学生四月份“读书量”的众数为 ;
(2)求本次所抽取学生四月份“读书量”的平均数;
(3)已知该校七年级有1200名学生,请你估计该校七年级学生中,四月份“读书量”为5本的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.如果点
的中点.如果点![]() 在线段
在线段![]() 上以
上以![]() 的速度由点
的速度由点![]() 向
向![]() 点运动,同时,点
点运动,同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向
向![]() 点运动.
点运动.

(1)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,经过1秒后,
的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由.
是否全等,请说明理由.
(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=kx+b的图象经过点(0,﹣2),(3,1).
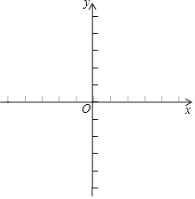
(1)求一次函数的表达式,并在所给直角坐标系中画出此函数的图象;
(2)根据图象回答:当x 时,y1=0;
(3)求直线y1=kx+b、直线y2=﹣2x+4与y轴围成的三角形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com