
| ||||||
|
| |||||
|
| |||||
| A | ||||||
| 1 |
| 64 |
| 1 |
| 64 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 64 |
| 63 |
| 64 |
| 63 |
| 64 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 256 |
| 1 |
| 512 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2100 |
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
 就反映了给一个方程配方的过程,
就反映了给一个方程配方的过程,查看答案和解析>>
科目:初中数学 来源: 题型:
 “数形结合”是一种极其重要的思想方法.例如,我们可以利用数轴解分式不等式
“数形结合”是一种极其重要的思想方法.例如,我们可以利用数轴解分式不等式| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 | ||
 |  | |
 |  | |
| A | ||
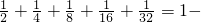 ______=______
______=______ ;
;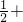
 +A+
+A+ .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| ||||||
|
| |||||
|
| |||||
| A | ||||||
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 256 |
| 1 |
| 512 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com