
正常水位时,抛物线拱桥下的水面宽为BC=20m,水面上升3m达到该地警戒水位DE时,桥下水面宽为10m.若以BC所在直线为x轴,BC的垂直平分线为y轴,建立如图所示的平面直角坐标系.

(1)求桥孔抛物线的函数关系式;
(2)如果水位以0.2m/h的速度持续上涨,那么达到警戒水位后,再过多长时间此桥孔将被淹没;
(3)当达到警戒水位时,一艘装有防汛器材的船,露出水面部分的宽为4m,高为0.75m,通过计算说明该船能否顺利通过此拱桥?
(1) 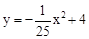 ;
(2)5;(3) 能通过,理由见解析.
;
(2)5;(3) 能通过,理由见解析.
【解析】
试题分析:(1)依题意得:B(-10,0),C(10,0),D(-5,3),E(5,3),应用待定系数法可得桥孔抛物线的函数关系式;
(2)首先求出警戒水位到桥面的距离,再求出时间t;
(3)求出x=2时的y值与0.75+3比较即可.
试题解析:(1)依题意得:B(-10,0),C(10,0),D(-5,3),E(5,3)
设函数解析式为:y=a(x-10)(x+10),
将 E(5,3)代入,得3=-75a,解得a=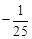 .
.
∴桥孔抛物线的函数关系式为y=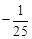 (x-10)(x+10),即
(x-10)(x+10),即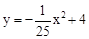 .
.
(2)∵t=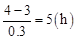 ,∴达到警戒水位后,再过5h此桥孔将被淹没.
,∴达到警戒水位后,再过5h此桥孔将被淹没.
(3)若x=2时,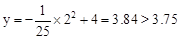 ,∴能通过.
,∴能通过.
考点:二次函数的应用.


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
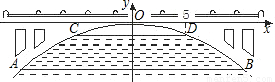
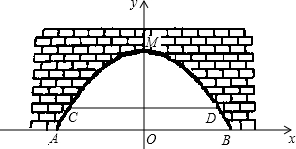 如图,是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.
如图,是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《二次函数》(03)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2012年北师大版初中数学九年级下2.7最大面积是多少练习卷(解析版) 题型:解答题
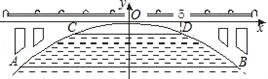
如图,有一座抛物线形拱桥,抛物线可用y=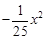 表示.在正常水位时水面AB 的宽为20m,如果水位上升3m时,水面CD的宽是10m.
表示.在正常水位时水面AB 的宽为20m,如果水位上升3m时,水面CD的宽是10m.
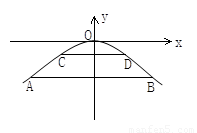
(1)在正常水位时,有一艘宽8m、高2.5m的小船,它能通过这座桥吗?
(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km(桥长忽略不计).货车正以每小时40km的速度开往乙地,当行驶1小时时, 忽然接到紧急通过:前方连降暴雨,造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处,当水位达到桥拱最高点O时,禁止车辆通行).试问:如果货车按原来的速度行驶,能否安全通过此桥?若能,请说明理由.若不能, 要使货车安全通过此桥,速度应超过每小时多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com