Question

某足球协会举办了一个足球联赛，其记分规则及奖励方案如表：

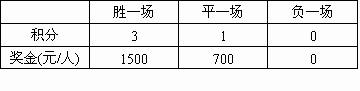
当比赛进行到第12轮结束(每队均需比赛12场)时，A队共积19分．

(1)请通过计算，判断A队胜、平、负各几场？

(2)若每赛一场，每名参赛队员均得出场费500元，设A队其中一名参赛队员所得的奖金与出场费的和为W(元)，试求W的最大值．

Answer 1

答案：
解析：

解：(1)设A队胜x场、平y场、负z场， 　　则　　从而 　　由题意知：x≥0，y≥0，z≥0，且x、y、z均为整数， 　　所以解得3≤x≤6 　　所以x可取4、5、6． 　　所以A队胜、平、负的场数有3种情况： 　　当x＝4时，y＝7，z＝1 　　当x＝5时，y＝4，z＝3 　　当x＝6时，y＝1，z＝5 　　(2)因为W＝(1500＋500)x＋(700＋500)y＋500z，将代入得W＝－600x＋19300．由于－600＜0所以W随x的减少而增大． 　　所以当x＝4时，W最大，W最大＝－600×4＋19300＝16900(元)

提示：

思路与技巧：在(2)中，是求奖金与出场费的和，要能挖掘题目中的隐含条件，找出不等关系，从而限制W的取值．