
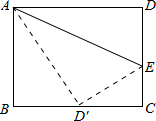
 如图,一个长方形的ABCD长为8cm,宽为6cm,E为边CD上的一点,现把Rt△ADE沿AE对折使得D点恰好落在边BC上的中点D′处.
如图,一个长方形的ABCD长为8cm,宽为6cm,E为边CD上的一点,现把Rt△ADE沿AE对折使得D点恰好落在边BC上的中点D′处.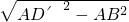 =2
=2 ,
, ,
,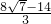 ,
,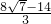 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图是一个长方形的铝合金窗框,其长为a(m),高为b(m),装有同样大的塑钢玻璃,当第②块向右拉到与第③块重叠
如图是一个长方形的铝合金窗框,其长为a(m),高为b(m),装有同样大的塑钢玻璃,当第②块向右拉到与第③块重叠| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 12、如图是一个长方形的土地,长50m,宽48m.由南到北,由东到西各修筑一条同样宽度的彩石路,要使空地的面积是2208m2,如果设小路宽为xm,根据题意所列的方程为
12、如图是一个长方形的土地,长50m,宽48m.由南到北,由东到西各修筑一条同样宽度的彩石路,要使空地的面积是2208m2,如果设小路宽为xm,根据题意所列的方程为查看答案和解析>>
科目:初中数学 来源: 题型:
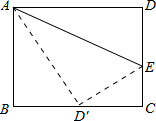 如图,一个长方形的ABCD长为8cm,宽为6cm,E为边CD上的一点,现把Rt△ADE沿AE对折使得D点恰好落在边BC上的中点D′处.
如图,一个长方形的ABCD长为8cm,宽为6cm,E为边CD上的一点,现把Rt△ADE沿AE对折使得D点恰好落在边BC上的中点D′处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com