
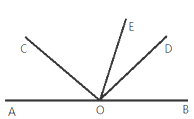
【题目】如图,点A、O、B在同一条直线上,∠AOC=∠BOD,OE是∠BOC的平分线.
(1)若∠AOC=46°,求∠DOE的度数;
(2)若∠DOE=30°,求∠AOC的度数.
【答案】(1)∠DOE=21 ;(2)∠AOC=40 .
【解析】试题分析:(1)由∠AOC=46°可求出∠BOC=134,由OE是∠BOC的平分线可求出∠BOE=67,然后根据∠DOE=∠BOE-∠BOD可求出∠DOE的度数;(2)设∠AOC的度数为x,则∠BOE=x+30 ,根据∠AOC+∠BOC=180°列方程求解.
解:(1)∵∠AOC=46°
∴∠BOC=180--∠AOC =180 -46 =134
又∵OE是∠BOC的平分线
∴∠BOE=![]() ∠BOC=67
∠BOC=67
又∵∠BOD=∠AOC= =46
∴∠DOE=∠BOE-∠BOD=67--46=21
(2)设∠AOC的度数为x,则∠BOD=x,则∠BOE=x+30
∵OE是∠BOC的平分线
∴∠BOC=2∠BOE=2(x+30 )
则有:x+2(x+30 )=180
解得:x=40
∴∠AOC=40


科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( ) ①a=3,b=4,c=5;
②a=6,∠A=45°;
③a=2,b=2,c=2 ![]() ;
;
④∠A=38°,∠B=52°.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个多边形的边数由原来的3增加到n时(n>3,且n为正整数),它的外角和( )
A. 增加(n﹣2)×180° B. 减小(n﹣2)×180° C. 增加(n﹣1)×180° D. 没有改变
查看答案和解析>>
科目:初中数学 来源: 题型:
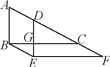
【题目】如图,将直角三角形ABC沿斜边AC的方向平移到三角形DEF的位置,DE交BC于点G,BG=4,EF=12,三角形BEG的面积为4,下列结论:①DE⊥BC;②三角形ABC平移的距离是4;③AD=CF;④四边形GCFE的面积为20,其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com