练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （2004•济宁）下列运算正确的是（ ）
    A．x•x3=x3
    B．x2+x2=x4
    C．（-4xy2）2=8x2y4
    D．（-2x2）（-4x3）=8x5
    【答案】分析：根据同底数幂的乘法，合并同类项的法则，积的乘方的性质，单项式的乘法法则，对各选项分析判断后利用排除法求解．
    解答：解：A、应为x•x3=x1+3=x4，故本选项错误；
    B、应为x2+x2=2x2，故本选项错误；
    C、应为（-4xy2）2=（-4）2x2（y2）4=16x2y4，故本选项错误；
    D、（-2x2）（-4x3）=（-2）×（-4）x2•x3=8x5，正确．
    故选D．
    点评：本题考查了同底数幂的乘法，合并同类项，积的乘方，单项式的乘法，熟练掌握性质和法则是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2004年全国中考数学试题汇编《二次函数》（05）（解析版） 题型：解答题

    （2004•济宁）已知抛物线y=x2-（2m-1）x+4m-6．
    （1）试说明对于每一个实数m，抛物线都经过x轴上的一个定点；
    （2）设抛物线与x轴的两个交点A（x1，0）和B（x2，0）（x1＜x2）分别在原点的两侧，且A、B两点间的距离小于6，求m的取值范围；
    （3）抛物线的对称轴与x轴交于点C，在（2）的条件下，试判断是否存在m的值，使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D，且被x轴截得的劣弧与是等弧？若存在，求出所有满足条件的m的值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2004年山东省济宁市中考数学试卷（解析版） 题型：解答题

    （2004•济宁）已知抛物线y=x2-（2m-1）x+4m-6．
    （1）试说明对于每一个实数m，抛物线都经过x轴上的一个定点；
    （2）设抛物线与x轴的两个交点A（x1，0）和B（x2，0）（x1＜x2）分别在原点的两侧，且A、B两点间的距离小于6，求m的取值范围；
    （3）抛物线的对称轴与x轴交于点C，在（2）的条件下，试判断是否存在m的值，使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D，且被x轴截得的劣弧与是等弧？若存在，求出所有满足条件的m的值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2004年全国中考数学试题汇编《一次函数》（04）（解析版） 题型：解答题

    （2004•济宁）我市某县素以“中国蒜都”著称．某运输公司计划用10辆汽车将甲、乙、丙三种大蒜共100吨运输到外地，按规定每辆车只能装同一种大蒜，且必须满载，每种大蒜不少于一车．
    （1）设用x辆车装运甲种大蒜，用y辆车装运乙种大蒜．根据下表提供的信息，求y与x之间的函数关系式，并求自变量x的取值范围；
    （2）设此次运输的利润为M（百元），求M与x的函数关系式及最大运输利润，并安排此时相应的车辆分配方案．
    大蒜品种甲乙丙
    每辆汽车的满载量（吨）81011
    运输每吨大蒜获利（元）2.22.12

    查看答案和解析>>

    科目：初中数学 来源：2004年全国中考数学试题汇编《一元二次方程》（05）（解析版） 题型：解答题

    （2004•济宁）阅读下面材料：
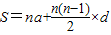    在计算1+4+7+10+13+16+19+22+25+28时，我们发现，从第一个数开始，以后的每个数与它的前一个数的差都是一个相同的定值，具有这种规律的一列数，求和时，除了直接相加外，我们还可以用公式来计算（公式中的S表示它们的和，n表示数的个数，a表示第一个数的值，d表示这个相差的定值）．那么S=1+4+7+10+13+16+19+22+25+28=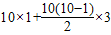=145．
    用上面的知识解决下列问题：
    我市某乡镇具有“中国北方乔木之乡”的美称，到2000年底这个镇已有苗木2万亩，为增加农民收入，这个镇实施“苗木兴镇”战略，逐年有计划地扩种苗木．从2001年起，以后每年又比上一年多种植相同面积的苗木；从2001年起每年卖出成苗木，以后每年又比上一年多卖出相同面积的苗木．下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据．
    年份2001年2002年2003年
    每年种植苗木的面积（亩）400050006000
    每年卖出成苗木的面积（亩）200025003000
    假设所有苗木的成活率都是100%，问到哪一年年底，这个镇的苗木面积达到5万亩？

    查看答案和解析>>

    科目：初中数学 来源：2010年黑龙江省鸡西市三校联考中考数学二模试卷（解析版） 题型：解答题

    （2004•济宁）我市某县素以“中国蒜都”著称．某运输公司计划用10辆汽车将甲、乙、丙三种大蒜共100吨运输到外地，按规定每辆车只能装同一种大蒜，且必须满载，每种大蒜不少于一车．
    （1）设用x辆车装运甲种大蒜，用y辆车装运乙种大蒜．根据下表提供的信息，求y与x之间的函数关系式，并求自变量x的取值范围；
    （2）设此次运输的利润为M（百元），求M与x的函数关系式及最大运输利润，并安排此时相应的车辆分配方案．
    大蒜品种甲乙丙
    每辆汽车的满载量（吨）81011
    运输每吨大蒜获利（元）2.22.12

    查看答案和解析>>

    同步练习册答案