
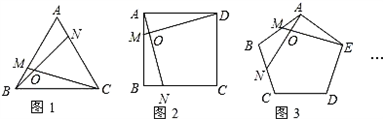
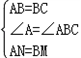 ,
,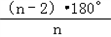 .
.

科目:初中数学 来源:活学巧练 八年级数学 下 题型:044
(1)阅读下题证明方法和过程,并填上推理根据.
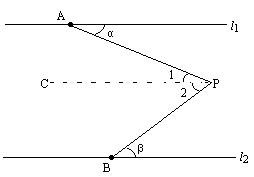
题目;如图,l1∥l2,点A,B分别在l1,l2上.求证∠P=∠α+∠β
证明:过点P作PC∥l1,
∴∠α=∠1( ).
∵l1∥l2(已知),
∴PC∥l2( ).
∴∠β=∠2( ).
∴∠1+∠2=∠α+∠β( ).
即∠P=∠α+∠β.
(2)某同学的证明思路与第1题不同,现只交待该同学为了证明需要所作的辅助线.领会他的思路,你能完成他的证明过程吗?请写出证明过程.
证明:过点A作AC∥PB交l2于C.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com