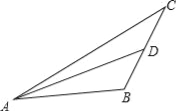
【题目】如图，在△ABC中（AB＞BC），AC=2BC，BC边上的中线AD把△ABC的周长分成60和40两部分，求AC和AB的长．

参考答案：

【答案】AC=48；AB=28

【解析】

试题分析：首先设BD=CD=x，AB=y，则AC=4x，然后分AC+CD=60，AB+BD=40和AC+CD=40，AB+BD=60两种情况分别求出x和y的值，然后看三角形的三边关系判定是否都符合条件.

试题解析：∵AD是BC边上的中线，AC=2BC， ∴BD=CD， 设BD=CD=x，AB=y，则AC=4x，

分为两种情况：①AC+CD=60，AB+BD=40， 则4x+x=60，x+y=40， 解得：x=12，y=28，

即AC=4x=48，AB=28；

②AC+CD=40，AB+BD=60， 则4x+x=40，x+y=60， 解得：x=8，y=52，

即AC=4x=32，AB=52，BC=2x=16， 此时不符合三角形三边关系定理；

综合上述：AC=48，AB=28．

关闭