练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．近年来，全国房价不断上涨，某县2014年2月份的房价平均每平方米为3600元，比2012年同期的房价平均每平方米上涨了500元，假设这两年该县房价的平均增长率均为x，则关于x 的方程为（　　）
    A．（1+x）2=500B．500（1+x）2=3600
    C．（3600-500）（1+x）=3600D．（3600-500）（1+x）2=3600

    分析 设这两年该县房价的平均增长率均为x，那么2013年4月份的房价平均每平方米为（3600-500）（1+x）元，2014年4月份的房价平均每平方米为（3600-500）（1+x）（1+x）元，然后根据某县2014年4月份的房价平均每平方米为3600元即可列出方程．

    解答 解：∵某县2014年4月份的房价平均每平方米为3600元，比2012年同期的房价平均每平方米上涨了500元，
    ∴2012年同期的房价平均每平方米3100元，假设这两年该县房价的平均增长率均为x，
    则关于x的方程为：（3600-500）（1+x）2=3600．
    故选D．

    点评 本题考查了求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

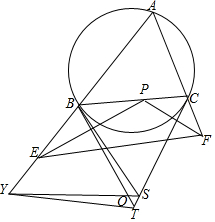    16．如图，在△ABC中，∠A=60°，P为线段BC（不含端点）上一点，E、F分别为射线AB、AC上的点，且BP=BE，CP=CF，△ABC的外接圆在B、C两点处的切线交于点S．设△EPF的外心为O，BO与CS交于点T，SO与直线AB交于点Y．求证：B、Y、T、S四点共圆．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列说法中，正确的是（　　）
    A．近似数3.20和近似数3.2都精确到十分位
    B．近似数3.20×103和近似数3.2×103都精确到百位
    C．近似数2千万和近似数2000万都精确到千万位
    D．近似数32.0和近似数3.2都精确到十分位

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，在边长为1个单位长度的小正方形组成的网格中，点A、B、C在小正方形的顶点上．
    （1）在图中画出与△ABC关于直线l成轴对称的△A′B′C′；
    （2）四边形ABB′A′的周长为$8+2\sqrt{5}$；
    （3）四边形ABCA′的面积为$\frac{17}{2}$；
    （4）在直线l上找一点P，使PA+PB的长最短，则这个最短长度为$\sqrt{17}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，已知正方形ABCD的边长AD=4，PC=1，CQ=DQ=2．求证：△ADQ∽△QCP．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：
    （1）2$\sqrt{12}$×（3$\sqrt{48}$-4$\sqrt{\frac{1}{8}}$-3$\sqrt{27}$）
    （2）（1+$\sqrt{2}$）（1-$\sqrt{2}$）+（$\sqrt{3}$+2）0+|2-$\sqrt{3}$|+$\frac{1}{\sqrt{3}-\sqrt{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，已知△ABC中，DE∥BC，AD=5，EC=2，BD=AE=x，求BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，在△ABC中，∠A=90°，BD是∠ABC的平分线，DE是BC的垂直平分线，求∠C的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．若x=3时，代数式ax3+2bx-7的值是8，那么x=-3时，代数式2ax3+4bx-7的值是-37．

    查看答案和解析>>

    同步练习册答案