练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    某二次函数的图象的顶点坐标（2，-1），且它的形状、开口方向与抛物线y=-x2相同，则这个二次函数的解析式为
    y=-（x-2）2-1
    y=-（x-2）2-1
    ．
    分析：根据抛物线的形状开口方向和抛物线的形状与a值有关，利用顶点式解析式写出即可．
    解答：解：∵抛物线的顶点坐标（2，-1），形状、开口方向与抛物线y=-x2相同，
    ∴这个二次函数的解析式为y=-（x-2）2-1．
    故答案为：y=-（x-2）2-1．
    点评：本题考查了二次函数图象与系数的关系，熟记抛物线y=ax2+bx+c中，a值确定抛物线的开口方向和抛物线的形状是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2012•黄冈模拟）如图，已知点F的坐标为（3，0），点A，B分别是以y轴为对称轴的某二次函数部分图象与x轴、y轴的交点，点P是此图象上的一动点．设点P的横坐标为x，PF的长为d，且d与x之间满足关系：d=5-
    3
    5
    x    （0≤x≤5），则此二次函数的解析式为
    y2=-
    16
    25
    x2+16
    y2=-
    16
    25
    x2+16
    ．

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：044

    　　某校研究性学习小组在研究有关二次函数及其图象的性质的问题时，发现了两个重要结论．一是发现抛物线y=ax2+2x+3(a≠0)，当实数a变化时，它的顶点都在某一条直线上．二是发现当实数a变化时，若把抛物线y=ax2+2x+3的顶点的横坐标减少，纵坐标增加，得到A点的坐标；若把顶点的横坐标增加，纵坐标增加，得到B点的坐标，则A、B两点一定仍在抛物线y=ax2+2x+3上．

    　　(1)请你协助探求出当实数a变化时，抛物线y=ax2+2x+3的顶点所在直线的解析式；

    　　(2)问题(1)中的直线上有一个点不是该抛物线的顶点，你能找出它来吗？并说明理由；

    　　(3)在他们第二个发现的启发下，运用“一般——特殊——一般”的思想，你还能发现什么？你能用数学语言将你的猜想表述出来吗？你的猜想能成立吗？若能成立，请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源：同步轻松练习　九年级数学下 题型：059

    某学校研究性学习小组在研究二次函数及其图象的问题时，发现了两个重要结论：

    ①抛物线y＝ax2＋2x＋3(a≠0)，当实数a变化时，它的顶点都在某条直线上；

    ②抛物线y＝ax2＋2x＋3的顶点横坐标减少，纵坐标增加得到点A；顶点横坐标增加，纵坐标增加得到点B，则A，B两点仍然在抛物线y＝ax2＋2x＋3上．

    (1)探索当实数a变化时，抛物线y＝ax2＋2x＋3的顶点所在直线的解析式；

    (2)问题(1)中的直线上有一个点不是抛物线的顶点，请你找出来，并说明理由；

    (3)请你参考第二个发现写出关于抛物线y＝ax2＋bx＋c顶点的结论，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

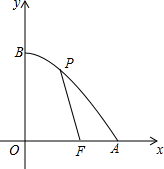    如图，已知点F的坐标为（3，0），点A，B分别是以y轴为对称轴的某二次函数部分图象与x轴、y轴的交点，点P是此图象上的一动点．设点P的横坐标为x，PF的长为d，且d与x之间满足关系：d=5-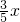数学公式（0≤x≤5），则此二次函数的解析式为________．

    查看答案和解析>>

    科目：初中数学 来源：2012年湖北省黄冈市中考数学调研试卷（4月份）（解析版） 题型：填空题

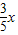    如图，已知点F的坐标为（3，0），点A，B分别是以y轴为对称轴的某二次函数部分图象与x轴、y轴的交点，点P是此图象上的一动点．设点P的横坐标为x，PF的长为d，且d与x之间满足关系：d=5-（0≤x≤5），则此二次函数的解析式为    ．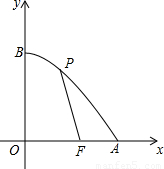

    查看答案和解析>>

    同步练习册答案