

分析 (1)根据平行线的性质、翻转变换的性质得到OE=BE,设BE=x,根据勾股定理列方程,解方程求出BE,根据三角形的面积公式计算即可;
(2)作DG⊥OA于G,交CB于F,根据三角形的面积公式求出DF,根据勾股定理求出EF,得到点D的坐标;
(3)分OP=OQ、OP=PQ、OQ=QP三种情况,根据等腰三角形的性质计算.
解答 解:(1)由翻转变换的性质可知,∠DOB=∠AOB,
∵BC∥OA,
∴∠CBO=∠AOB,
∴∠DOB=∠CBO,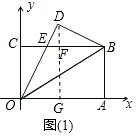
∴OE=BE,
设BE=x,则CE=8-x,OE=BE=x,
∵42+(8-x)2=x2,
∴x=5,即BE=5,
S△OEB=$\frac{1}{2}BE•OC$=$\frac{1}{2}×5×4=10$;
(2)如图(1),作DG⊥OA于G,交CB于F,则DF⊥CB,
∵OE=BE=5,
∴CE=DE=3,
由勾股定理得,DB=$\sqrt{B{E}^{2}-D{E}^{2}}$=4,
$\frac{1}{2}$×DE×DB=$\frac{1}{2}$×BE×DF,
解得,DF=$\frac{12}{5}$,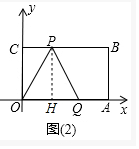
由勾股定理得EF=$\frac{9}{5}$,
则CF=3+$\frac{9}{5}$=$\frac{24}{5}$,$DG=\frac{12}{5}+4=\frac{32}{5}$,
∴点D的坐标为($\frac{24}{5}$,$\frac{32}{5}$);
(3)当OP=OQ时,CP=$\sqrt{O{P}^{2}-O{C}^{2}}$=3,
则点P的坐标为(3,4),
当PO=PQ时,作PH⊥OA于H,
则OH=$\frac{1}{2}$OQ=2.5,
∴点P的坐标为(2.5,4),
当QO=QP时,点P的坐标为(2,4)或(8,4),
∴△OQP是等腰三角形,点P的坐标为(3,4),(2.5,4)(2,4),(8,4).
点评 本题考查的是矩形的性质、等腰三角形的判定和性质以及勾股定理的应用,掌握相关的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
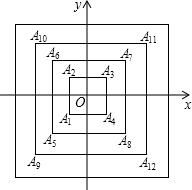 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A51的坐标是(13,13).
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A51的坐标是(13,13).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两人利用不同的交通工具,沿同一路线分别从A、B两地同时出发匀速前往C地(B在A、C两地的途中).设甲、乙两车距A地的路程分别为y甲、y乙(千米),行驶的时间为x(小时),y甲、y乙与x之间的函数图象如图所示.
甲、乙两人利用不同的交通工具,沿同一路线分别从A、B两地同时出发匀速前往C地(B在A、C两地的途中).设甲、乙两车距A地的路程分别为y甲、y乙(千米),行驶的时间为x(小时),y甲、y乙与x之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com