(1)解:∵四边形ABCD是矩形,
∴∠D=90°,
由折叠的性质可得:AB′=AB=5,
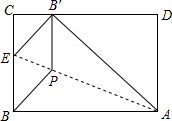
在Rt△ADB′中,B′D=
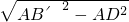
=3;
(2)证明:由折叠的性质可得:BP=B′P,BE=B′E,
∵BP=BE,
∴BP=B′P=B′E=BE,
∴四边形BPB′E的形状为菱形;
(3)存在.
∵四边形BPB′E的形状为菱形,
∴BE∥B′P,BP=B′P,
∴BC⊥CD,
∴B′P⊥CD,
∴点P到边CD的距离与到点B的距离相等,
设BP=x,
则B′E=x,
∵B′C=CD-B′D=5-3=2,CE=BC-BE=4-x,
在Rt△B′CE中,B′E
2=CE
2+B′C
2,
∴x
2=(4-x)
2+2
2,
解得:x=2.5,
∴此相等距离的值为2.5.
分析:(1)由折叠的性质,可得AB′=AB=5,又由矩形纸片ABCD中,AB=5,AD=4,根据勾股定理即可求得B′D的长;
(2)由BP=BE与折叠的性质,即可证得BP=B′P=B′E=BE,则可得四边形BPB′E的形状为菱形;
(3)由四边形BPB′E的形状为菱形,可得点P到边CD的距离与到点B的距离相等,然后设BP=x,由勾股定理可得:x
2=(4-x)
2+2
2,解此方程即可求得答案.
点评:此题考查了矩形的性质、折叠的性质、勾股定理以及菱形的判定与性质.此题难度较大,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

 矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点B落在边CD上的B′处,折痕为AE,点P是AE上的一点,且BP=BE,连接B′P.
矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点B落在边CD上的B′处,折痕为AE,点P是AE上的一点,且BP=BE,连接B′P.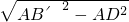 =3;
=3;

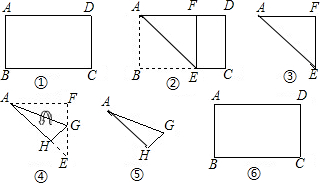
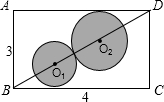 如图,矩形纸片ABCD中,AB=3cm,BC=4cm,若要在该纸片中剪下两个外切的圆⊙O1和⊙O2,要求⊙O1和⊙O2的圆心均在对角线BD上,且⊙O1和⊙O2分别与BC、AD相切,则O1O2的长为( )
如图,矩形纸片ABCD中,AB=3cm,BC=4cm,若要在该纸片中剪下两个外切的圆⊙O1和⊙O2,要求⊙O1和⊙O2的圆心均在对角线BD上,且⊙O1和⊙O2分别与BC、AD相切,则O1O2的长为( )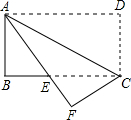 如图,在矩形纸片ABCD中,将矩形纸片沿着对角线AC折叠,使点D落在点F处,设AF与BC相交于点E.
如图,在矩形纸片ABCD中,将矩形纸片沿着对角线AC折叠,使点D落在点F处,设AF与BC相交于点E.