
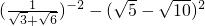
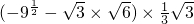
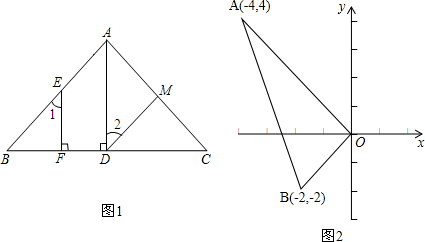
 +
+ )2-(
)2-( -
- )2=(3+6
)2=(3+6 +36)-(5-10
+36)-(5-10 +10)=39+6
+10)=39+6 -15+10
-15+10 =24+16
=24+16 ;
; -
- ×
× ×
× =-
=- -
- ;
; (2+4)×6-
(2+4)×6- ×4×4-
×4×4- ×2×2=8.
×2×2=8. +
+ )2-(
)2-( -
- )2,然后利用完全平方公式展开后合并即可;
)2,然后利用完全平方公式展开后合并即可;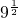 =3,然后根据二次根式的乘法进行计算;
=3,然后根据二次根式的乘法进行计算;

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
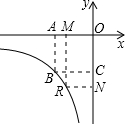 如图,正方形OABC的面积是4,点B在反比例函数y=
如图,正方形OABC的面积是4,点B在反比例函数y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com