

| 解:(1)C(0,2) , D(1,2); | |
| (2)由y=-2x+4求得B(0,4),A(0,2), 如图①,折叠后点B与点A重合, 则△ACD≌△BCD,BD=DA, 由(1)得D的坐标为(1,2), 设点C的坐标为(0,m)(m>0), 则BC=OB-OC=4-m, 于是AC=BC=4-m, 在Rt△AOC中,由勾股定理,得AC2=OC2+OA2, 即(4-m)2=m2+22, 解得 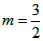 , ,∴点C的坐标为 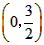 ,D的坐标为(1,2); ,D的坐标为(1,2); |
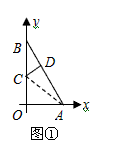 |
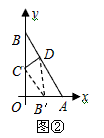
| (3)如图②,折叠后点B落在OA边上的点为B', 且B'D∥OB, 则△B'CD≌△BCD,∠OCB'=∠CB'D, 又∵∠CBD=∠CB'D, ∴∠OCB'=∠CBD, 有CB'∥BA, ∴Rt△COB'∽Rt△BOA, 有 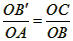 , ,得OC=2OB', 在Rt△B'OC中, 设OB'=x0(x>0),则OC=2x0, 则B'C=BC=OB-OC=4-2x0, 在Rt△B'OC中,由勾股定理,得B'C2=OC2+OB'2, ∴(4-2x0)2=(2x0)2+x02, 得x20+16x0-16=0, 解得 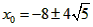 , ,∵x0>0, ∴ 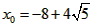 , ,∴点C的坐标为 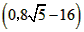 , ,∵B'D∥OB, 则可得点D的横坐标为 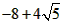 , ,设点D的纵坐标为n, ∵点D在直线y=-2x+4上, ∴ 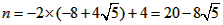 , ,∴点D的坐标为 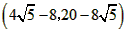 。 。 |
 |


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
 的动点,折叠直角三角形纸片OAB,使折叠后点B与点B'重合,折痕与边OB交于点C,与边AB交于点D.
的动点,折叠直角三角形纸片OAB,使折叠后点B与点B'重合,折痕与边OB交于点C,与边AB交于点D.查看答案和解析>>
科目:初中数学 来源:新海实验中学2008年中考第一次模拟考试数学试题 题型:013
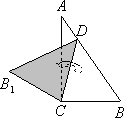
如图,将一个直角三角形纸片(∠ACB=90°),沿线段CD折叠,使点B落在点B1处,若∠ACB1=70°,则∠ACD的度数为
A.10°
B.15°
C.20°
D.25°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
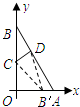 的动点,折叠直角三角形纸片OAB,使折叠后点B与点B'重合,折痕与边OB交于点C,与边AB交于点D.
的动点,折叠直角三角形纸片OAB,使折叠后点B与点B'重合,折痕与边OB交于点C,与边AB交于点D.查看答案和解析>>
科目:初中数学 来源:2011年《海峡教育报》初中数学综合练习(二)(解析版) 题型:解答题
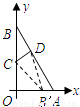
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com