
 如图,已知,点A(0,0)、B(4$\sqrt{3}$,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
如图,已知,点A(0,0)、B(4$\sqrt{3}$,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )| A. | $\frac{\sqrt{3}}{{2}^{2015}}$ | B. | $\frac{\sqrt{3}}{{2}^{2016}}$ | C. | $\frac{\sqrt{3}}{{2}^{2017}}$ | D. | $\frac{\sqrt{3}}{{2}^{2019}}$ |
分析 根据题目已知条件可推出,AA1=$\frac{\sqrt{3}}{2}$OC,B1A2=$\frac{1}{2}$A1B1,依此类推,第n个等边三角形的边长等于$\frac{1}{{2}^{n}}$×4$\sqrt{3}$,于是得到结论.
解答 解:如图,∵点C(0,4),∠ABC=30°,
∴OB=4$\sqrt{3}$.
∴BC=8,
∴∠OBC=30°,∠OCB=60°.
而△AA1B1为等边三角形,∠A1AB1=60°,
∴∠COA1=30°,则∠CA1O=90°.
在Rt△CAA1中,AA1=$\frac{\sqrt{3}}{2}$OC=2$\sqrt{3}$.
同理得:B1A2=$\frac{1}{2}$A1B1=$\frac{1}{{2}^{2}}$×4$\sqrt{3}$,
依此类推,第n个等边三角形的边长等于$\frac{1}{{2}^{n}}$×4$\sqrt{3}$,
∴第2017个等边三角形的边长等于$\frac{1}{{2}^{2017}}$×4$\sqrt{3}$=$\frac{\sqrt{3}}{{2}^{2015}}$,
故选:A.
点评 本题主要考查等边三角形的性质及解直角三角形,从而归纳出边长的规律是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{2}{3x}$ | B. | y=$\frac{2}{3}$x-1 | C. | y=$\frac{3}{4}$x | D. | y=$\frac{1}{2}$(x-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
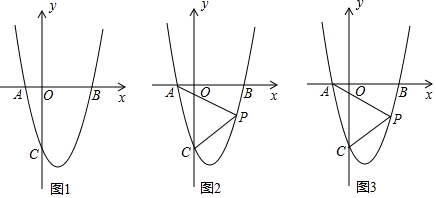
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
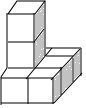 如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )
如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )| A. | 正视图的面积最大 | B. | 左视图的面积最大 | ||
| C. | 俯视图的面积最大 | D. | 三个视图的面积一样大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com