
 与x轴的两个交点A、B,与y轴交于点C,A点坐标为(
与x轴的两个交点A、B,与y轴交于点C,A点坐标为(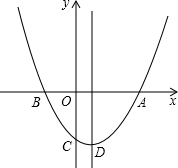 4,0),C点坐标(0,-4).
4,0),C点坐标(0,-4).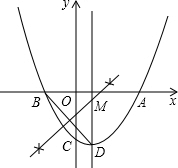 解:(1)依题意,有:
解:(1)依题意,有: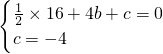 ,
,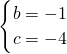
 x2-x-4;
x2-x-4;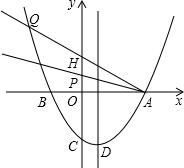 (3)依题意可知:∠PAB=∠QAB=22.5°,设直线AQ与y轴交于H,∠HAO=45°,
(3)依题意可知:∠PAB=∠QAB=22.5°,设直线AQ与y轴交于H,∠HAO=45°,
 ,
, ;
;

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
| 3 | 2 |
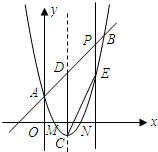 作x轴的垂线交抛物线于点E,使四边形DCEP为平行四边形?若存在,请求出该平行四边形的面积;若不存在,说明理由.
作x轴的垂线交抛物线于点E,使四边形DCEP为平行四边形?若存在,请求出该平行四边形的面积;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知m,n是方程x2-6x+5=0的两个实数根,且m<n抛物线y=-x2+bx+c.的图象经过点A(m,0),B(0,n).
已知m,n是方程x2-6x+5=0的两个实数根,且m<n抛物线y=-x2+bx+c.的图象经过点A(m,0),B(0,n).查看答案和解析>>
科目:初中数学 来源:2013届浙江省杭州市江南实验学校九年级5月月考数学试卷(带解析) 题型:解答题
如图,抛物线 与x轴的两个交点A、B,与y轴交于点C,A点坐标为(4,0),C点坐标(0,-4).
与x轴的两个交点A、B,与y轴交于点C,A点坐标为(4,0),C点坐标(0,-4).
(1)求抛物线的解析式;
(2)用直尺和圆规作出△ABC的外接圆⊙M,(不写作法,保留作图痕迹),并求⊙M的圆心M的坐标;
查看答案和解析>>
科目:初中数学 来源:2012年内蒙古巴彦淖尔市磴口县诚仁中学中考数学模拟试卷(一)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省九年级5月月考数学试卷(解析版) 题型:解答题
如图,抛物线 与x轴的两个交点A、B,与y轴交于点C,A点坐标为(4,0),C点坐标(0,-4).
与x轴的两个交点A、B,与y轴交于点C,A点坐标为(4,0),C点坐标(0,-4).

(1)求抛物线的解析式;
(2)用直尺和圆规作出△ABC的外接圆⊙M,(不写作法,保留作图痕迹),并求⊙M的圆心M的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com