
 ,求x;
,求x;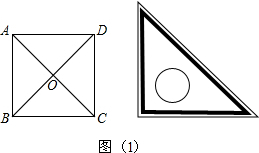
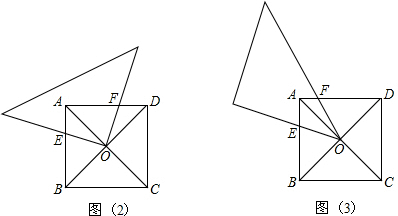
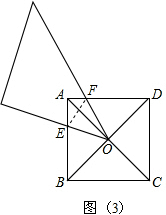
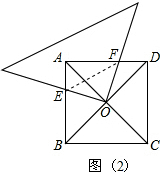 解:(1)∵正方形ABCD,
解:(1)∵正方形ABCD,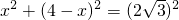 ,
,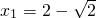 ,
,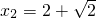 .
.
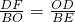 ,
,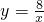 .
.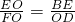 ,
,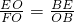 ,
,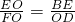 ,而BO=DO,代入比例式中,再根据已知条件现在可以证明△EOF∽△EBO,从而得到∠FEO=∠OEB,然后根据角平分线的性质知道点O到EF、BE的距离相等,也就可以判断直线EF与正方形的内切圆相切了.
,而BO=DO,代入比例式中,再根据已知条件现在可以证明△EOF∽△EBO,从而得到∠FEO=∠OEB,然后根据角平分线的性质知道点O到EF、BE的距离相等,也就可以判断直线EF与正方形的内切圆相切了.

科目:初中数学 来源: 题型:
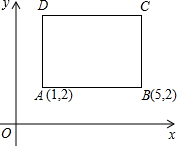 如图,四边形ABCD是一正方形,已知A(1,2),B(5,2)
如图,四边形ABCD是一正方形,已知A(1,2),B(5,2)查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
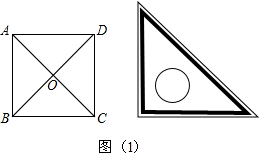
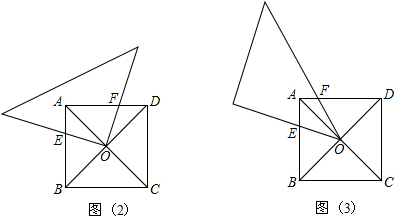
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
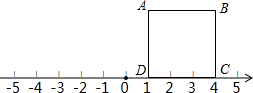
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com