练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知，图23-3-18、图23-3-19分别是6×6正方形网格上的两个轴对称图形(阴影部分)，其面积分别为S1、S2(网格中最小的正方形面积为一个平方单位)，请观察图形并解答下列问题.

    　 　　

    图23-3-18　　　　　　 图23-3-19　　　　 图23-3-20

    (1)求S1∶S2的值.?

    (2)请在图23-3-20的网格上画出一个面积为8平方单位的中心对称图形.
    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知抛物线y=-
    23
    （x+2）2+k与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，C点在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x2-10x+16=0的两个根．
    （1）求A、B、C三点的坐标；
    （2）在平面直角坐标系内画出抛物线的大致图象并标明顶点坐标；
    （3）连AC、BC，若点E是线段AB上的一个动点（与A、B不重合），过E作EF∥AC交BC于F，连CE，设AE=m，△CEF的面积为S，求S与m的函数关系式，并写出自变量m的取值范围；
    （4）在（3）的基础上说明S是否存在最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，已知∠ABC=90°，△ABE是等边三角形，点P为射线BC上任意一点（点P与点B不重合），连接AP，将线段AP绕点A逆时针旋转60°得到线段AQ，连接QE并延长交射线BC于点F．
    （1）如图2，当BP=BA时，∠EBF=
     
    °，猜想∠QFC=
     
    °；
    （2）如图1，当点P为射线BC上任意一点时，猜想∠QFC的度数，并加以证明；
    （3）已知线段AB=2
    		3
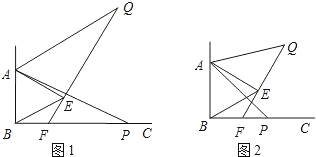    ，设BP=x，点Q到射线BC的距离为y，求精英家教网y关于x的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

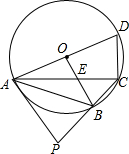    如图，四边形ABCD内接于⊙O，已知直径AD=2
    		3
    ，∠ADC=60°，∠ACB=45°，连接OB交AC于点E．
    （1）求CE：AE的值；
    （2）在CB的延长线上取一点P，使PB=2BC，试判断直线PA和⊙O的位置关系，并证明你的结论；
    （3）在（2）的情况下，求线段PA、PB与
    AB
    所围成的图形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

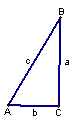
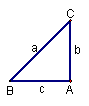
    在一个三角形中，如果一个角是另一个角的2倍，我们称这种三角形为倍角三角形．如图23-1，倍角△ABC中，∠A=2∠B，∠A、∠B、∠C的对边分别记为a,b,c，倍角三角形的三边a,b,c有什么关系呢？让我们一起来探索．


    （图23-1）　　 （图23-2）　　 （图23-3）　　　　 （图23-4）

    （1）我们先从特殊的倍角三角形入手研究。请你结合图形填空：

    三角形

    角的已知量

    图23-2

    ∠A=2∠B=

    图23-3

    ∠A=2∠B=

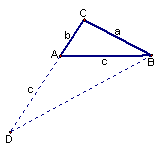
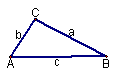
    （2）如图23-4，对于一般的倍角△ABC，若∠CAB=2∠CBA ，∠CAB、∠CBA、∠C的对边分别记为a,b,c，a,b,c，三边有什么关系呢？请你作出猜测，并结合图23-4给出的辅助线提示加以证明．

    （3）请你运用（2）中的结论解决下列问题：若一个倍角三角形的两边长为5，6，求第三边长． （直接写出结论即可）（原创）

    查看答案和解析>>

    同步练习册答案