
分析 根据题意列出函数关系式即可;
①根据三角形的三边关系定理得出x+x>26-2x;②根据三角形的边长不能为负数和0得出y=26-2x>0,x>0,求出符合以上条件的解集即可.
解答 解:底边y与腰长x之间的函数关系式是y=26-2x;
①根据三角形的三边关系定理得:x+x>y,
即x+x>26-2x,
x>$\frac{13}{2}$,
②y=26-2x>0,x>0
解得:$\frac{13}{2}$<x<13,
即自变量x的取值范围是$\frac{13}{2}$<x<13,
故答案为:y=26-2x;$\frac{13}{2}$<x<13.
点评 本题考查了一次函数的应用和三角形的三边关系定理,关键是能根据题意得出不等式x+x>12-2x,y=12-2x>0,x>0.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
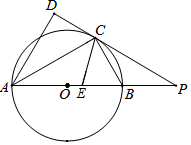 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com