
 如图,在一个圆弧形门拱中,拱高AB的长为1m,跨度CD的长为4m,求这个门拱的半径.
如图,在一个圆弧形门拱中,拱高AB的长为1m,跨度CD的长为4m,求这个门拱的半径. 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:
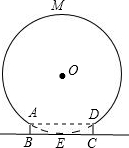 我们在园林游玩时,常见到如图所示的圆弧形的门,若圆弧所在圆与地面BC相切于E点,四边形ABCD是一个矩形.已知AB=
我们在园林游玩时,常见到如图所示的圆弧形的门,若圆弧所在圆与地面BC相切于E点,四边形ABCD是一个矩形.已知AB=2-
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源:2009-2010学年河南省开封五中九年级(上)期中数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009-2010学年山东省枣庄市东方国际学校九年级(上)第五次月考数学试卷(解析版) 题型:解答题
 米,BC=1米.
米,BC=1米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com