
 ⊙O的直径,已知PA=OA=4,AC=CD.
⊙O的直径,已知PA=OA=4,AC=CD. 解:(1)连接OC、BC、AD,
解:(1)连接OC、BC、AD, ,
, ;
; =
=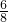 =
= .
.

科目:初中数学 来源: 题型:
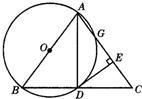 50、如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连接AD,并过点D作DE⊥AC,垂足为E.根据以上条件写出三个正确结论(除AB=AC,AO=BO,∠ABC=∠ACB外)是:
50、如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连接AD,并过点D作DE⊥AC,垂足为E.根据以上条件写出三个正确结论(除AB=AC,AO=BO,∠ABC=∠ACB外)是:查看答案和解析>>
科目:初中数学 来源: 题型:
 25、已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.
25、已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.查看答案和解析>>
科目:初中数学 来源: 题型:
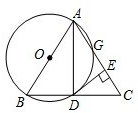 如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连接AD,并过点D作DE⊥AC,垂足为E.根据以上条件写出三个正确结论(除AB=AC,AO=BO,∠ABC=∠ACB外)是:
如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连接AD,并过点D作DE⊥AC,垂足为E.根据以上条件写出三个正确结论(除AB=AC,AO=BO,∠ABC=∠ACB外)是:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.
已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.查看答案和解析>>
科目:初中数学 来源:2010-2011学年四川省达州市渠县中学九年级(上)第二学月数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com