

分析 (1)先由△ABC和△AFE的形状大小完全相同得到AB=AF,∠ABC=∠AFE,再根据旋转的性质得∠BAE=∠FAC=α,于是可利用“ASA”证明△ABM≌△AFN,所以AM=AN;
(2)在Rt△ABC中利用勾股定理计算出BC=5,再由菱形性质得AB∥PF,得到∠ANF=∠BAC=90°,接着根据△ABM≌△AFN得到∠AMB=∠ANF=90°,则可根据面积法计算出AM=$\frac{12}{5}$,然后在Rt△AMC中利用勾股定理计算出MC=$\frac{16}{5}$,最后根据三角形面积公式求解.
解答 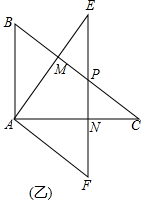 (1)证明:∵△ABC和△AFE的形状大小完全相同,
(1)证明:∵△ABC和△AFE的形状大小完全相同,
∴AB=AF,∠ABC=∠AFE,
∵Rt△AEF绕A点按顺时针方向旋转角α(0°<α<90°),如图乙,
∴∠BAE=∠FAC=α,
在△ABM和△AFN中,
$\left\{\begin{array}{l}{∠ABM=∠AFN}\\{AB=AF}\\{∠BAM=∠FAN}\end{array}\right.$,
∴△ABM≌△AFN(ASA),
∴AM=AN;
(2)在Rt△ABC中,∵AB=3,AC=4,
∴BC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵四边形ABPF是菱形,
∴AB∥PF,
∴∠ANF=∠BAC=90°,
∵△ABM≌△AFN,
∴∠AMB=∠ANF=90°,
∵$\frac{1}{2}$AM•BC=$\frac{1}{2}$AB•AC,
∴AM=$\frac{3×4}{5}$=$\frac{12}{5}$,
在Rt△AMC中,∵AC=4,AM=$\frac{12}{5}$,
∴MC=$\sqrt{{4}^{2}-(\frac{12}{5})^{2}}$=$\frac{16}{5}$,
∴S△AMC=$\frac{1}{2}$AM•MC=$\frac{1}{2}$×$\frac{12}{5}$×$\frac{16}{5}$=$\frac{96}{25}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.旋转有三要素:旋转中心; 旋转方向; 旋转角度.也考查了全等三角形的判定与性质、菱形性质和勾股定理.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/千克) | 2 | 2.2 | 2.4 | 2.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
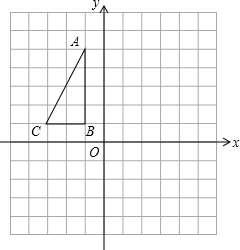 如图,在平面直角坐标系中,ABC的顶点的坐标分别为A(-1,5)、B(-1,1)、C(-3,1).将△ABC向右平移2个单位、再向下平移4个单位得到△A1B1C1;将△ABC绕原点O旋转180°得到△A2B2C2
如图,在平面直角坐标系中,ABC的顶点的坐标分别为A(-1,5)、B(-1,1)、C(-3,1).将△ABC向右平移2个单位、再向下平移4个单位得到△A1B1C1;将△ABC绕原点O旋转180°得到△A2B2C2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com