
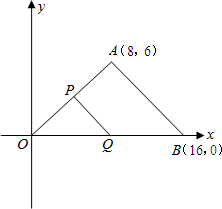
 (秒)表示移动时间,当这两点中有一点到达自己的终点时,另一点也停止运动.
(秒)表示移动时间,当这两点中有一点到达自己的终点时,另一点也停止运动.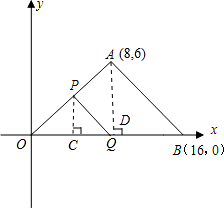 解:(1)由已知得
解:(1)由已知得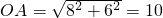 ,
,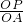 =
=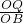 ,
,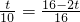 ,得:
,得:
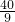 秒时PQ∥AB;
秒时PQ∥AB;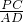 =
=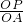 ,
,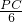 =
= ,
,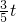 ,y=
,y= OQ,PC=
OQ,PC= (16-2t),
(16-2t), t=-
t=-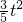 +
+ t;
t;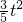 +
+ t;
t;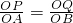 ,据此列出关于t的方程,并解方程;
,据此列出关于t的方程,并解方程;

 53随堂测系列答案
53随堂测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com