
| 5 |
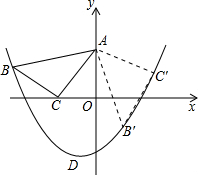 ,使点C的坐标为(-1,0),点A在y轴上,点B在抛物线y=ax2+ax-2上.
,使点C的坐标为(-1,0),点A在y轴上,点B在抛物线y=ax2+ax-2上.| 5 |
| 5 |
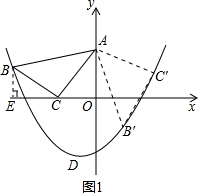 解:(1)如图1,做BE⊥x轴,
解:(1)如图1,做BE⊥x轴,| 5 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
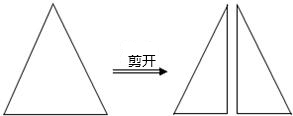
 24、如图,有一腰长为5,底边长为4的等腰三角形纸片,现沿着等腰三角形底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中,是四边形的共有( )
24、如图,有一腰长为5,底边长为4的等腰三角形纸片,现沿着等腰三角形底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中,是四边形的共有( )查看答案和解析>>
科目:初中数学 来源:陕西 题型:填空题
查看答案和解析>>
科目:初中数学 来源:第25章《图形的变换》中考题集(23):25.3 轴对称变换(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2006年广西钦州市中考数学试卷(大纲卷)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com