
 如图,在△ABC中,AB=AC,AE是高,AF是△ABC外角∠CAD的平分线.
如图,在△ABC中,AB=AC,AE是高,AF是△ABC外角∠CAD的平分线.分析 (1)根据角平分线的作法作∠AEC的平分线EN即可;
(2)先根据题意得出AE平分∠BAC,再由AF是△ABC外角∠CAD的平分线可得出∠EAM=90°,根据EN是∠AEC的平分线可得出∠AEM=45°,据此可得出结论.
解答 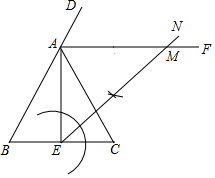 解:(1)如图,射线EN即为所求;
解:(1)如图,射线EN即为所求;
(2)△ADF是等腰直角三角形.
在△ABC中,
∵AB=AC,AE⊥BC,
∴AE平分∠BAC,
∴∠EAC=$\frac{1}{2}$∠BAC.
∵AF平分∠CAD,
∴∠CAF=$\frac{1}{2}$∠CAD,
∴∠EAF=$\frac{1}{2}$(∠BAC+∠CAD)=$\frac{1}{2}$×180°=90°,
∵∠AEC=90°,EN是∠AEC的平分线,
∴∠AEM=45°,
∴∠AME=45°,
∴AE=AM,即△AEM是等腰直角三角形.
点评 本题考查的是作图-基本作图,熟知角平分线的作法是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
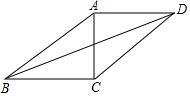 在?ABCD中,对角线AC、BD交于点E,AC⊥BC,AB=8,∠ABC=30°,
在?ABCD中,对角线AC、BD交于点E,AC⊥BC,AB=8,∠ABC=30°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2017年3月全国两会胜利召开,某学校就两会期间出现频率最高的热词:A.蓝天保卫战,B.不动产保护,C.经济增速,D.简政放权等进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
2017年3月全国两会胜利召开,某学校就两会期间出现频率最高的热词:A.蓝天保卫战,B.不动产保护,C.经济增速,D.简政放权等进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com