
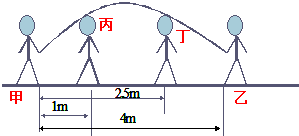
 在跳绳时,绳甩到最高处的形状可近似的看作抛物线.如图,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米;学生丙的身高是1.5米,距甲拿绳的手水平距离1米,绳子甩到最高处时,刚好通过他的头顶.
在跳绳时,绳甩到最高处的形状可近似的看作抛物线.如图,正在甩绳的甲、乙两名学生拿绳的手间距为4米,距地面均为1米;学生丙的身高是1.5米,距甲拿绳的手水平距离1米,绳子甩到最高处时,刚好通过他的头顶.
 x2+
x2+ x+
x+ ,
, ×1.52+
×1.52+ ×1.5+
×1.5+ =
=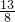 ,
,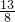 m;
m; x2+
x2+ x+
x+ =-
=- (x-1)2+
(x-1)2+ ,
, ),
), <1.7,
<1.7,

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com