
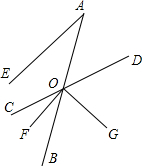
 如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.
如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
 如图,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线.
如图,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:
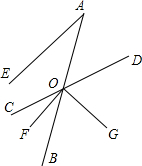 如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.
如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知射线DM与直线BC交于点A,AB∥DE.
如图,已知射线DM与直线BC交于点A,AB∥DE.查看答案和解析>>
科目:初中数学 来源:2011-2012学年河南漯河市直中学七年级下期中联合测试数学试卷(带解析) 题型:解答题
如图,已知射线DM与直线BC交于点A,AB∥DE.
(1)若当 ,
, 时,问把EC绕点E再旋转多大角度时,可判定MD∥EC,请你设计出两种方案,并画出草图(旋转后若EC与AB相交,则交点用
时,问把EC绕点E再旋转多大角度时,可判定MD∥EC,请你设计出两种方案,并画出草图(旋转后若EC与AB相交,则交点用 表示).
表示).
(2)若将EC绕点E逆时针旋转 时,点C与点A恰好重合,请画出草图,并在图中找出同位角、内错角各两对(先用数字标出角,再回答).
时,点C与点A恰好重合,请画出草图,并在图中找出同位角、内错角各两对(先用数字标出角,再回答).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com