
如图所示,某学校拟建一个含内接矩形的菱形花坛(花坛为轴对称图形).矩形的四个顶点分别在菱形四条边上,菱形ABCD的边长AB=4米,∠ABC=60°.设AE=x米(0<x<4),矩形EFGH的面积为S米2.
(1)求S与x的函数关系式;
(2)学校准备在矩形内种植红色花草,四个三角形内种植黄色花草.已知红色花草的价格为20元/米2,黄色花草的价格为40元/米2.当x为何值时,购买花草所需的总费用最低,并求出最低总费用(结果保留根号)?
解:(1)连接AC、BD,
∵花坛为轴对称图形,
∴EH∥BD,EF∥AC。
∴△BEF∽△BAC。
∵∠ABC=60°,
∴△ABC、△BEF是等边三角形。
∴EF=BE=AB﹣AE=4﹣x,
在Rt△AEM中,∠AEM=∠ABD=30°,
则EM=AEcos∠AEM= x,∴EH=2EM=
x,∴EH=2EM= x.
x.
∴S=(4﹣x)× x=﹣
x=﹣ x2+4
x2+4 x。
x。
(2)易求得菱形ABCD的面积为8 cm2,
cm2,
由(1)得,矩形ABCD的面积为 x2,则可得四个三角形的面积为(8
x2,则可得四个三角形的面积为(8 +
+ x2﹣4
x2﹣4 x),
x),
设总费用为W,
则W=20(﹣ x2+4
x2+4 x)+40(8
x)+40(8 +
+ x2﹣4
x2﹣4 x)=20
x)=20 x2﹣80
x2﹣80 x+320
x+320
=20 (x﹣2)2+240
(x﹣2)2+240 。
。
∵0<x<4,∴当x=2时,W取得最小,W最小=240 元。
元。
∴当x为2时,购买花草所需的总费用最低,最低费用为240 元。
元。
解析试题分析:(1)连接AC、BD,根据轴对称的性质,可得EH∥BD,EF∥AC,△BEF为等边三角形,从而求出EF,在Rt△AEM中求出EM,继而得出EH,这样即可得出S与x的函数关系式。
(2)根据(1)的答案,可求出四个三角形的面积,设费用为W,则可得出W关于x的二次函数关系式,利用配方法求最值即可。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
如图,抛物线y=ax2+bx+3与x轴相交于点A(﹣1,0)、B(3,0),与y轴相交于点C,点P为线段OB上的动点(不与O、B重合),过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F,点D在y轴正半轴上,OD=2,连接DE、OF.
(1)求抛物线的解析式;
(2)当四边形ODEF是平行四边形时,求点P的坐标;
(3)过点A的直线将(2)中的平行四边形ODEF分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在直角体系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3。取BO的中点D,连接CD、MD和OC。
(1)求证:CD是⊙M的切线;
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使 ?若存在,求出点Q的坐标;若不存在,请说明理由。
?若存在,求出点Q的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,二次函数的图象与x轴相交于点A(﹣3,0)、B(﹣1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx﹣4k(k≠0)的图象过点P交x轴于点Q.
(1)求该二次函数的解析式;
(2)当点P的坐标为(﹣4,m)时,求证:∠OPC=∠AQC;
(3)点M,N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M,N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.连接AN,当△AMN的面积最大时,
①求t的值;
②直线PQ能否垂直平分线段MN?若能,请求出此时点P的坐标;若不能,请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年四川自贡14分)如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA= .
.
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
铜仁市某电解金属锰厂从今年1月起安装使用回收净化设备(安装时间不计),这样既改善了环境,又降低了原料成本,根据统计,在使用回收净化设备后的1至x月的利润的月平均值w(万元)满足w=10x+90.
(1)设使用回收净化设备后的1至x月的利润和为y,请写出y与x的函数关系式.
(2)请问前多少个月的利润和等于1620万元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数y=ax2+bx+c(a≠0)的图象经过点(1,0),(5,0),(3,﹣4).
(1)求该二次函数的解析式;
(2)当y>﹣3,写出x的取值范围;
(3)A、B为直线y=﹣2x﹣6上两动点,且距离为2,点C为二次函数图象上的动点,当点C运动到何处时△ABC的面积最小?求出此时点C的坐标及△ABC面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y=a(x﹣h)2+k经过点A(0,1),且顶点坐标为B(1,2),它的对称轴与x轴交于点C.
(1)求此抛物线的解析式.
(2)在第一象限内的抛物线上求点P,使得△ACP是以AC为底的等腰三角形,请求出此时点P的坐标.
(3)上述点是否是第一象限内此抛物线上与AC距离最远的点?若是,请说明理由;若不是,请求出第一象限内此抛物线上与AC距离最远的点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线 过点A(1,0),顶点为B,且抛物线不经过第三象限。
过点A(1,0),顶点为B,且抛物线不经过第三象限。
(1)使用a、c表示b;
(2)判断点B所在象限,并说明理由;
(3)若直线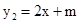 经过点B,且于该抛物线交于另一点C(
经过点B,且于该抛物线交于另一点C( ),求当x≥1时y1的取值范围。
),求当x≥1时y1的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com