练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    ?ABCD中一条对角线分∠A为35°和45°，则∠B=________度．

    100
    分析：求出∠BAD度数，根据平行四边形性质得出AD∥BC，推出∠B+∠BAD=180°即可．
    解答：
    解：∵?ABCD中一条对角线分∠A为35°和45°，
    ∴∠BAD=80°，
    ∵四边形BACD是平行四边形，
    ∴BC∥AD，
    ∴∠B+∠BAD=180°，
    ∴∠B=100°，
    故答案为：100．
    点评：本题考查了平行四边形性质和平行线性质的应用，关键是求出∠BAD度数和得出∠B+∠BAD=180°．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    图1是只有一组对角为直角的四边形（我们规定这一类四边形的集合为M），连接它的两个非直角顶点的线段叫做这个四边形的“直径”（相当于经过这个四边形的四个顶点的圆的直径）．
    （1）识图：如图1，四边形ABCD的直径是线段
    BD
    BD
    ；
    （2）判断：如图2，在坐标系中（网格小方格的单位长为1）的四边形EFGH是否为M中的四边形？给出简要说明；
    （3）思考、操作并解决问题：在图2中找到一个点P，使四边形EFPH为M中的四边形，并且这个四边形用一条直线分割成两块后可以拼成一个正方形．要求：写出点P的坐标、画出分割线，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

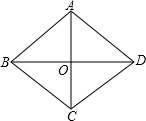    如图，在菱形ABCD中，对角线AC、BD相交于点O，则：
    （1）AB=AD=
    BC
    BC
    =
    CD
    CD
    ，即菱形的
    四条边
    四条边
    相等．
    （2）图中的等腰三角形有
    △ABD、△ABC、△ADC、△BCD
    △ABD、△ABC、△ADC、△BCD
    ，直角三角形有
    △DOA、△AOB、△COB、△COD
    △DOA、△AOB、△COB、△COD
    ，△AOD≌
    △AOB
    △AOB
    ≌
    △COB
    △COB
    ≌
    △COD
    △COD
    ，由此可以得出菱形的对角线
    垂直平分
    垂直平分
    ，每一条对角线
    平分一组对角
    平分一组对角
    ．
    （3）菱形是轴对称图形，它的对称轴是
    对角线所在的直线
    对角线所在的直线
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在正方形ABCD中，E是CD边上的中点，AC与BE相交于点F，连接DF.(注：正方形的四边相等，四个角都是直角，每一条对角线平分一组对角).  

    1.(1) 在不增加点和线的前提下,直接写出图中所有的全等三角形;

    2.连接AE,试判断AE与DF的位置关系,并证明你的结论;

    3.延长DF交BC于点M,试判断BM与MC的数量关系，并说明理由。

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在正方形ABCD中，E是CD边上的中点，AC与BE相交于点F，连接DF.(注：正方形的四边相等，四个角都是直角，每一条对角线平分一组对角).  
    【小题1】(1) 在不增加点和线的前提下,直接写出图中所有的全等三角形;
    【小题2】连接AE,试判断AE与DF的位置关系,并证明你的结论;
    【小题3】延长DF交BC于点M,试判断BM与MC的数量关系，并说明理由。

    查看答案和解析>>

    科目：初中数学 来源：2013届河北省承德地区八年级上学期期中考试数学卷 题型：解答题

    如图，在正方形ABCD中，E是CD边上的中点，AC与BE相交于点F，连接DF.(注：正方形的四边相等，四个角都是直角，每一条对角线平分一组对角).  

    1.(1) 在不增加点和线的前提下,直接写出图中所有的全等三角形;

    2.连接AE,试判断AE与DF的位置关系,并证明你的结论;

    3.延长DF交BC于点M,试判断BM与MC的数量关系，并说明理由。

     

    查看答案和解析>>

    同步练习册答案