
分析 (1)本题涉及负整数指数幂、二次根式化简、特殊角的三角函数值3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)根据完全平方公式和平方差公式化简,然后把a、b的值代入计算..
解答 解:(1)(-$\frac{1}{3}$)-2-$\sqrt{12}$+6cos30°
=9-2$\sqrt{3}$+6×$\frac{\sqrt{3}}{2}$
=9-2$\sqrt{3}$+3$\sqrt{3}$
=9+$\sqrt{3}$;
(2)(a+b)(a-b)-(a-2b)2
=a2-b2-a2+4ab-4b2
=4ab-5b2,
当a=2,b=-1时,原式=4×2×(-1)-5×1=-13.
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、二次根式、特殊角的三角函数值等考点的运算.同时考查了整式的混合运算,涉及了完全平方公式、平方差公式、合并同类项的知识点.注意运算顺序以及符号的处理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
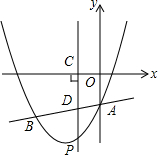 如图,抛物线y=x2+bx+c与直线y=$\frac{1}{2}$x-3交于A、B两点,其中点A在y轴上,点B坐标为(-4,-5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
如图,抛物线y=x2+bx+c与直线y=$\frac{1}{2}$x-3交于A、B两点,其中点A在y轴上,点B坐标为(-4,-5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
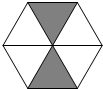 如图所示的六边形广场由若干个大小完全相同的黑色和白色正三角形组成,一只小鸟在广场上随机停留,刚好落在黑色三角形区域的概率为$\frac{1}{3}$.
如图所示的六边形广场由若干个大小完全相同的黑色和白色正三角形组成,一只小鸟在广场上随机停留,刚好落在黑色三角形区域的概率为$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对我国初中学生视力状况的调查 | |
| B. | 对量子科学通信卫星上某种零部件的调查 | |
| C. | 对一批节能灯管使用寿命的调查 | |
| D. | 对“最强大脑”节目收视率的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com