
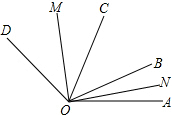
 如图,∠AOB:∠BOC:∠COD=2:3:4,射线ON,OM分别平分∠AOB与∠COD,又∠MON=90°,求∠AOB的度数.
如图,∠AOB:∠BOC:∠COD=2:3:4,射线ON,OM分别平分∠AOB与∠COD,又∠MON=90°,求∠AOB的度数. 分析 设∠AOB的度数为2x,则∠BOC的度数为3x,∠COD的度数为4x,根据射线ON,OM分别平分∠AOB与∠COD即可得出∠BON=x、∠COM=2x,再根据∠MON=∠COM+∠BOC+∠BON=90°即可得出关于x的一元一次方程,解方程即可求出x的值,将其代入∠AOB=2x即可得出结论.
解答 解:设∠AOB的度数为2x,则∠BOC的度数为3x,∠COD的度数为4x,
∵射线ON,OM分别平分∠AOB与∠COD,
∴∠BON=x,∠COM=2x,
∵∠MON=90°,
∴∠COM+∠BOC+∠BON=2x+3x+x=6x=90°,
∴x=15°,2x=30°.
答:∠AOB的度数为30°.
点评 本题考查了角平分线的定义以及解一元一次方程,根据角与角的关系找出关于x的一元一次方程是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
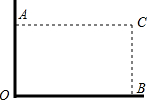 如图,一个商人要建一个矩形的仓库,仓库的两边是住房墙,另外两边用20m长的建筑材料围成,且仓库的面积为96m2.
如图,一个商人要建一个矩形的仓库,仓库的两边是住房墙,另外两边用20m长的建筑材料围成,且仓库的面积为96m2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一条直线上有两条射线 | B. | 以B为端点的射线有射线AB和BA | ||
| C. | 延长线段AB相当于反向延长线段BA | D. | 一条直线只能经过两个点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ,已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ,已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{18{a^3}}$ | B. | $\frac{{2\sqrt{8a}}}{3a}$ | C. | $\sqrt{3{a^2}+4{b^2}}$ | D. | $\sqrt{\frac{b}{a}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com