如图，在平面直角坐标系中，函数
的图象
是第一、三象限的角平分线．
(1)实验与探究：由图观察易知A（0，2）关于直线的对称点
的坐标为（2，0），请在图中分别标明B（5，3） 、C（-2，5） 关于直线的对称点
、
的位置，并写出它们的坐标: 、 ；
(2)归纳与发现：结合图形观察以上三组点的坐标，
你会发现：坐标平面内任一点P（m，n）关于第一、三象限的角平分线的对称点
的坐标为 .
科目：初中数学 来源： 题型：解答题
暑假期间，两位家长计划带领若干名学生去旅游，他们联系了报价均为每人1000元的两家旅行社。经协商，甲旅行社的优惠条件是：两位家长全额收费，学生都按7折收费；乙旅行社的优惠条件是：学生、家长都按8折收费。假设这两位家长带领
名学生去旅行，甲、乙旅行社的收费分别为
，
（1）、写出与的函数关系式。
（2）、学生人数在什么情况下，选择甲旅行社更省钱？
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，一次函数y=kx+b(k≠ 0)与反比例函数
(m≠0)的图象有公共点A(1，2),D(a,-1)．直线 轴于点N(3，0)，与一次函数和反比例 函数的图象分别交于点B，C．
(1) 求一次函数与反比例函数的解析式；
(2) 求△ABC的面积。
(3) 根据图象回答，在什么范围时，一次函数的值大于反比例函数的值。
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
某蔬菜经销商到蔬菜种植基地采购一种蔬菜，经销商一次性采购蔬菜的采购单价y（元/千克）与采购量x（千克）之间的函数关系图象如图中折线AB——BC——CD所示（不包括端点A）．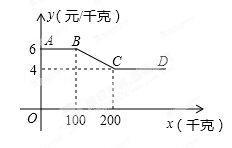
（1）当100＜x＜200时，直接写y与x之间的函数关系式．
（2）蔬菜的种植成本为2元/千克，某经销商一次性采购蔬菜的采购量不超过200千克，当采购量是多少时，蔬菜种植基地获利最大，最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，已知反比例函数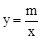
（m是常数，m≠0），一次函数y＝ax＋b（a、b为常数，a≠0），其中一次函数与x轴，y轴的交点分别是A（－4，0），B（0，2）．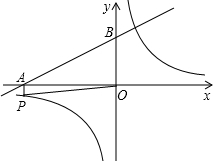
（1）求一次函数的关系式；
（2）反比例函数图象上有一点P满足：①PA⊥x轴；②PO＝
（O为坐标原点），求反比例函数的关系式；
（3）求点P关于原点的对称点Q的坐标，判断点Q是否在该反比例函数的图象上．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
“母亲节”到了，八年级（1）班班委发起慰问烈属王大妈的活动，决定在“母亲节”期间全班同学利用课余时间去卖鲜花筹集慰问金．已知同学们从花店按每支1.2元买进鲜花，并按每支3元卖出．
（1）求同学们卖出鲜花的销售额
（元）与销售量
（支）之间的函数关系式；
（2）若从花店购买鲜花的同时，还总共用去40元购买包装材料，求所筹集的慰问金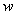
（元）与销售量（支）之间的函数关系式；若要筹集不少于500元的慰问金，则至少要卖出鲜花多少支？（慰问金=销售额－成本）
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
点P（x，y）在第一象限，且x+y=10，点A的坐标为（8，0），设原点为O，△OPA的面积为S．
（1）求S与x的函数关系式，写出x的取值范围，画出这个函数图象；
（2）当S=12时，求点P的坐标；
（3）△OPA的面积能大于40吗？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
做服装生意的王老板经营甲、乙两个店铺，每个店铺在同一段时间内都能售出A，B两种款式的服装合计30件，并且每售出一件A款式和B款式服装，甲店铺获毛利润分别为30元和40元，乙店铺获毛利润分别为27元和36元。某日王老板进货A款式服装35件，B款式服装25件。怎样分配给每个店铺各30件服装，使得在保证乙店铺毛利润不小于950元的前提下，王老板获取的总毛利润最大？最大的总毛利润是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
） (2) （n，m）
，
为何值时，它的图象经过原点；
）.