
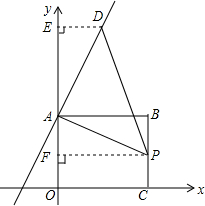
 如图,矩形ABCO位于直角坐标系平面,O为原点,A、C分别在坐标轴上,B的坐标为(8,5),线段BC上有一动点P,已知点D在第一象限
如图,矩形ABCO位于直角坐标系平面,O为原点,A、C分别在坐标轴上,B的坐标为(8,5),线段BC上有一动点P,已知点D在第一象限分析 (1)①点D在直线y=2x+6上,分三种情况进行讨论:①D为直角顶点;②A为直角顶点;③P为直角顶点,分别求出D坐标即可;
(2)点D在直线y=2x-6上,也需分三种情况讨论;①A为直角顶点;②P为直角顶点;③D为直角顶点,分别结合全等三角形的判定和性质进行求出D坐标即可.
解答 解:易知:A(0,6),C(8,0),AB=8,OA=BC=6;
则点A正好位于直线y=2x+6上;
(1)当点D位于直线y=2x+6上时,分三种情况:
①点P为直角顶点,显然此时点D位于第四象限,不合题意;
②点D为直角顶点,那么∠DAP=45°,结合图形2可知:∠DAB>45°,
而点P位于线段BC上,故不存在这样的等腰直角三角形;
③点A为直角顶点,如图1;
过D作DE⊥y轴于E,则△ADE≌△APB,得:AE=AB=8;
即点D的纵坐标为14,代入y=2x+6中,可求得点D(4,14);
(2)当点D位于直线y=2x-6上时,分三种情况:
①点A为直角顶点,结合图形2可知,此种情况显然不合题意;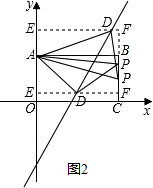
②点D为直角顶点,分两种情况:
(i)点D在矩形AOCB的内部时,如图2,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,设D(x,2x-6);
则OE=2x-6,AE=6-(2x-6)=12-2x,DF=EF-DE=8-x;
则△ADE≌△DPF,得DF=AE,即:
12-2x=8-x,x=4;
∴D(4,2);
(ii)点D在矩形AOCB的外部时,设D(x,2x-6);
则OE=2x-6,AE=OE-OA=2x-6-6=2x-12,DF=EF-DE=8-x;
同1可知:△ADE≌△DPF⇒AE=DF,即:
2x-12=8-x,x=$\frac{20}{3}$;
∴D($\frac{20}{3}$,$\frac{22}{3}$);
③点P为直角顶点,显然此时点D位于矩形AOCB的外部,如图3所示;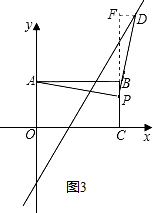 设点D(x,2x-6),则CF=2x-6,BF=2x-6-6=2x-12;
设点D(x,2x-6),则CF=2x-6,BF=2x-6-6=2x-12;
易证得△APB≌△PDF,得:
AB=PF=8,PB=DF=x-8;
故BF=PF-PB=8-(x-8)=16-x;
联立两个表示BF的式子可得:
2x-12=16-x,即x=$\frac{28}{3}$;
∴D($\frac{28}{3}$,$\frac{38}{3}$);
综合上面六种情况可得:存在符合条件的等腰直角三角形;
且D点的坐标为:(4,2),($\frac{20}{3}$,$\frac{22}{3}$),($\frac{28}{3}$,$\frac{38}{3}$).
点评 此题属于一次函数综合题,涉及的知识有:点的坐标、矩形的性质、一次函数的应用、等腰直角三角形以及全等三角形等相关知识的综合应用,需要考虑的情况较多,难度较大,熟练掌握性质及运算法则是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{1\frac{9}{16}}$=$\frac{5}{4}$ | B. | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ | C. | $\sqrt{0.25}$=0.05 | D. | -$\sqrt{-49}$-(-7)=7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com