
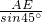 =
= AE,AC=
AE,AC= =
= AB,
AB, AB-
AB- AE=
AE= (AB-AE)=
(AB-AE)= BE,
BE, :1;
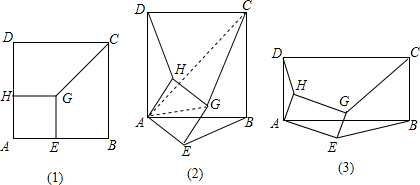
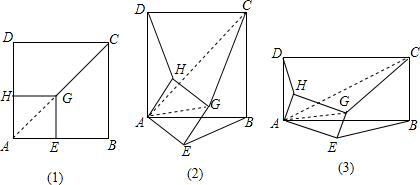
:1; ,∠DAC=∠HAG=45°,
,∠DAC=∠HAG=45°, ,
,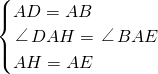 ,
, :1;
:1; ,∠DAC=∠HAG,
,∠DAC=∠HAG, ,
, :n.
:n. BE,即可求得HD:GC:EB的值;
BE,即可求得HD:GC:EB的值;

 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
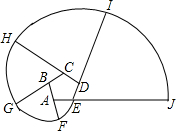 如图,五边形ABCDE是正五边形,曲线EFGHIJ…叫做“正五边形ABCDE的渐开线”,其中EF、FG、GH、HI、IJ…的圆心依次按A、B、C、D、E循环,它们依次相连接.如果AB=1,那么曲线EFGHIJ的长度为
如图,五边形ABCDE是正五边形,曲线EFGHIJ…叫做“正五边形ABCDE的渐开线”,其中EF、FG、GH、HI、IJ…的圆心依次按A、B、C、D、E循环,它们依次相连接.如果AB=1,那么曲线EFGHIJ的长度为查看答案和解析>>
科目:初中数学 来源: 题型:
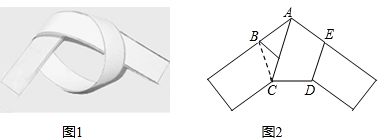
| A、1:2 | ||
| B、1:3 | ||
C、(
| ||
D、(3-
|
查看答案和解析>>
科目:初中数学 来源: 题型:
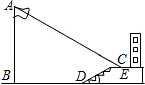 梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆AB的高度.如图,当阳光从正西方向照射过来时,旗杆AB的顶端A的影子落在教学楼前的坪地C处,测得影长CE=2m,DE=4m,BD=20m,DE与地面的夹角α=30度.在同一时刻,测得一根长为1m的直立竹竿的影长恰为4m.根据这些数据求旗杆AB的高度.(可能用到的数据:
梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆AB的高度.如图,当阳光从正西方向照射过来时,旗杆AB的顶端A的影子落在教学楼前的坪地C处,测得影长CE=2m,DE=4m,BD=20m,DE与地面的夹角α=30度.在同一时刻,测得一根长为1m的直立竹竿的影长恰为4m.根据这些数据求旗杆AB的高度.(可能用到的数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知:正△ABC,AO⊥BC于H,⊙O切AB为D,
如图,已知:正△ABC,AO⊥BC于H,⊙O切AB为D,
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
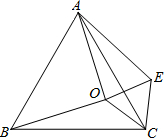 如图,点O是正△ABC内一点,∠AOB=90°,∠BOC=α,将△BOC绕点C顺时针旋转60°得到△AEC,连接OE
如图,点O是正△ABC内一点,∠AOB=90°,∠BOC=α,将△BOC绕点C顺时针旋转60°得到△AEC,连接OE| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com