
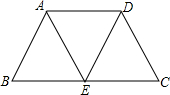
 如图,已知在平行四边形ABED中,AE是对角线,∠B=∠EAD,延长BE至点C,使EC=BE,并连接DC.
如图,已知在平行四边形ABED中,AE是对角线,∠B=∠EAD,延长BE至点C,使EC=BE,并连接DC.
 =2
=2 ,
, ×(4+8)×4=24.
×(4+8)×4=24.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
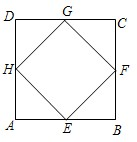 四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.
四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图,四边形EFGH是正方形ABCD的内接平行四边形,且已知正方形ABCD的边长为4.查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:022
已知如图所示,在平行四边ABCD中,对角线相交于点O,已知AB=24cm,BC=18cm,△AOB的周长是54cm那么△AOD的周长是________cm.

查看答案和解析>>
科目:初中数学 来源:同步训练与评价·数学·八年级·上 题型:044
阅读材料,解答问题.
①如图(1)已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,过A作AG⊥EB,垂足为G,AG交BD于F,则OE=OF理由是:∵四边开ABCD是正方形,∴∠BOE=∠AOF=![]() ,BO=AO.又∵AG⊥EB,∠1+∠3=
,BO=AO.又∵AG⊥EB,∠1+∠3=![]() =∠2+∠3∴∠1=∠2,∴Rt△BOE≌Rt△AOF解答此题后某同学产生了如下猜想:对上述命题,若点E在AC的延长线上,AG⊥EB,AG交EB的延长线于G,AG的延长线交DB的延长线于F,其它条件不变,如图,则仍有OE=OF.问猜想所得的结论是否成立,请说明理由.
=∠2+∠3∴∠1=∠2,∴Rt△BOE≌Rt△AOF解答此题后某同学产生了如下猜想:对上述命题,若点E在AC的延长线上,AG⊥EB,AG交EB的延长线于G,AG的延长线交DB的延长线于F,其它条件不变,如图,则仍有OE=OF.问猜想所得的结论是否成立,请说明理由.

②已知:E、F分别是平行四边形ABCD的边AD和BC的中点,并且2AB=BC,G是AF和BE的交点,H是CE和DF的交点.(1)试探求四边形GFHE的形状;并说明理由.(2)若四边形GFHE是正方形,平行四边形ABCD应满足什么条件?

查看答案和解析>>
科目:初中数学 来源: 题型:022
已知如图所示,在平行四边ABCD中,对角线相交于点O,已知AB=24cm,BC=18cm,△AOB的周长是54cm那么△AOD的周长是________cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com