
【题目】曲阜限制“三小车辆”出行后,为方便市民出行,准备为![]() 、
、![]() 、
、![]() 、
、![]() 四个村建一个公交车站
四个村建一个公交车站![]() .
.

(1)请问:公交站![]() 建在何处才能使它到4个村的距离之和
建在何处才能使它到4个村的距离之和![]() 最小,请在图一中找出点
最小,请在图一中找出点![]() ;
;
(2)请问:公交站![]() 建在何处才能使它到道路
建在何处才能使它到道路![]() 、
、![]() 、
、![]() 的距离相等,请在图二中找出点
的距离相等,请在图二中找出点![]() 并加以说明.
并加以说明.
【答案】(1)见解析;(2)见解析
【解析】
(1)公交站P是AC与BD的交点,要证这点到四点的距离最小,可以证明除这点以外的点到四点的距离大于这点到四点的距离;
(2)公交站![]() 是∠ABC与∠DCB角平分线的交点,由角平分线性质定理可知,角平分线上的点到这个角两边的距离相等.
是∠ABC与∠DCB角平分线的交点,由角平分线性质定理可知,角平分线上的点到这个角两边的距离相等.
解:(1)应建在AC,BD连线的交点P处,如图一,

理由:如下图,若不建在P处,建在P1处,由三角形两边之和大于第三边可知,
 ,
,
即P1A+P1C+P1B+P1D>AC+BD,
故结论成立应建在P处.
即P1A+P1C+P1B+P1D>AC+BD.
故结论成立应建在P处.
(2)应建在∠ABC与∠DCB角平分线的交点处,如图二,

理由:由角平分线性质定理可知,角平分线上的点到这个角两边的距离相等.
所以点P道路![]() 、
、![]() 、
、![]() 的距离相等.
的距离相等.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示的是丽水市统计局公布的2010~2013年全社会用电量的折线统计图.

(1)根据统计图填写统计表:
2010~2013年丽水市全社会用电量统计表
年份 | 2010 | 2011 | 2012 | 2013 |
全社会用电量 (单位:亿KW·h) | 13.33 |
(2)根据丽水市2010年至2013年全社会用电量统计数据,求2011~2013年全社会用电量的年平均增长率(保留到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60 m到达点C,测得点B在点C的北偏东60°方向,如图②.
(1)求∠CBA的度数;
(2)求出这段河的宽(结果精确到1 m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).

① ②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个30°的角BAC与角MON,顶点A在射线ON上某处,现保持角MON不动,将角BAC绕点A以每秒15°的速度顺时针旋转,边AB、AC分别与边OM交于点P、Q,当AC∥OM时,交点Q消失旋转结束。设运动时间为t秒(t>0).


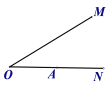

(1)当t=2秒时,OP:PQ= ;
(2)在运动的过程中,△APQ能否成为等腰三角形?若能,请利用备用图,直接写出此时的运动时间;
(3)在(2)中判断△OAQ的形状,并选择其中的一个说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
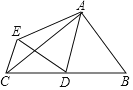
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论:

①CE=CF;
②线段EF的最小值为![]() ;
;
③当AD=1时,EF与半圆相切;
④当点D从点A运动到点O时,线段EF扫过的面积是4![]() .
.
其中正确的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的顶点![]() ,且经过点
,且经过点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() 两点.
两点.

(1)求直线![]() 和该抛物线的解析式;
和该抛物线的解析式;
(2)如图1,点![]() 是抛物线上的一个动点,且在直线
是抛物线上的一个动点,且在直线![]() 的上方,过点
的上方,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)如图2,![]() 轴交
轴交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一个动点,直线
之间的一个动点,直线![]() 、
、![]() 与
与![]() 分别交于
分别交于![]() 、
、![]() ,当点
,当点![]() 运动时,求
运动时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能写成![]() 的形式(其中a,b均为自然数),则称之为婆罗摩笈多数,比如7和31均是婆罗摩笈多数,因为7=22+3×12,31=22+3×32。
的形式(其中a,b均为自然数),则称之为婆罗摩笈多数,比如7和31均是婆罗摩笈多数,因为7=22+3×12,31=22+3×32。
(1)请证明:28和217都是婆罗摩笈多数。
(2)请证明:任何两个婆罗摩笈多数的乘积依旧是婆罗摩笈多数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民夏季(5月—10月)阶梯电价价目如右表.李叔叔家8月份用电500度,他家这个月要电费___元.张阿姨家8月份缴纳电费249.4元,她家这个月用电___度.(不计公共分摊部分).
阶梯 | 电量(度) | 电价/度 |
第一档 | 0—260部分 | 0.59元 |
第二档 | 261—600部分 | 0.64元 |
第三档 | 601度以上部分 | 0.89元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com